Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`a)` Gọi đường thẳng cần tìm là: `y=ax+b` `(\Delta)`
Có: `3x-4y+5=0`
`<=>y=3/4x+5/4`
Vì `\Delta //// d=>a=3/4;b ne 5/4`
Thay `a=3/4` và `A(-2;1)` vào `\Delta` có:
`1=3/4.(-2)+b<=>b=5/2` (t/m)
`=>\Delta: y=3/4x+5/2`
`b)` Có: `R=d(A;d)=[|3.(-1)-4.1+5|]/[\sqrt{3^2+(-4)^2}]=2/5`
`=>` Ptr đường tròn có `R=2/5` và tâm `A(-2;1)` là:
`(x+2)^2+(y-1)^2=4/25`

`a)` Gọi đường thẳng `\Delta` song song với `d` là: `3x+4y+c=0` `(c ne 5)`
Mà `I in \Delta`
`=>2.1+4.3+c=0<=>c=-14` (t/m)
`=>PTTQ` của `\Delta` là: `3x+4y-14=0`
`b)` Có: `R=d(I;d)=[|3.1+4.3+5|]/[\sqrt{3^2+4^2}]=4`
`=>` Ptr đường tròn tâm `I` bán kinh `R=4` là:
`(x-1)^2+(y-3)^2=16`

Do đường tròn tiếp xúc với đường thẳng d tại H nên IH và d vuông góc với nhau.
Đường thẳng IH: qua I( -1; 3) và nhận VTCP ( 3; -4) nên có VTPT n → ( 4;3) nên có phương trình là :
4( x + 1) + 3( y-3) =0 hay 4x+ 3y – 5= 0.
Ta có: IH và d cắt nhau tại H nên tọa độ của H là nghiệm hệ:
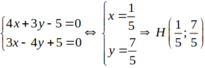
Chọn B.

Do I thuộc d nên tọa độ có dạng: \(I\left(3a-8;-a\right)\)
(C) qua A nên \(IA=R\)
\(\overrightarrow{AI}=\left(3a-6;-a-1\right)\Rightarrow R=\sqrt{10a^2-34a+37}\)
(C) tiếp xúc d' nên:
\(R=d\left(I;d'\right)\Leftrightarrow\sqrt{10a^2-34a+37}=\frac{\left|3\left(3a-8\right)+4a+10\right|}{\sqrt{3^2+\left(-4\right)^2}}\)
\(\Leftrightarrow5\sqrt{10a^2-34a+37}=\left|13a-14\right|\)
\(\Leftrightarrow25\left(10a^2-34a+37\right)=\left(13a-14\right)^2\)
\(\Leftrightarrow81a^2-486a+729=0\)
\(\Leftrightarrow a=3\Rightarrow\left\{{}\begin{matrix}I\left(1;-3\right)\\R=5\end{matrix}\right.\)
Phương trình: \(\left(x-1\right)^2+\left(y+3\right)^2=25\)