Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Gọi M ( x 0 ; 2 + 3 x 0 - 1 ) ∈ C , x 0 ≠ 1 .
Phương trình tiếp tuyến tại M có dạng
∆ : y = - 3 x 0 - 1 2 ( x - x 0 ) + 2 + 3 x 0 - 1
+ Giao điểm của ∆ với tiệm cận đứng là A ( 1 ; 2 + 6 x 0 - 1 )
+ Giao điểm của ∆ với tiệm cận ngang là B( 2x0-1; 2).
Ta có S ∆ I A B = 1 2 I A . I B = 1 2 . 6 x 0 - 1 . 2 . x 0 - 1 = 2 . 3 = 6
Tam giác IAB vuông tại I có diện tích không đổi nên chu vi tam giác IAB đạt giá trị nhỏ nhất khi
IA=IB 
+Với x 0 = 1 + 3 thì phương trình tiếp tuyến là ∆ : y = - x + 3 + 2 3 . Suy ra
d O , ∆ = 3 + 2 3 2
+ Với x 0 = 1 - 3 thì phương trình tiếp tuyến là ∆ : y = - x + 3 - 2 3 . Suy ra
d O , ∆ = - 3 + 2 3 2
Vậy khoảng cách lớn nhất là 3 + 2 3 2 gần với giá trị 5 nhất trong các đáp án.
Chọn D.

\(x=2\) là TCĐ, \(y=1\) là TCN \(\Rightarrow I\left(2;1\right)\)
\(y'=\dfrac{-4}{\left(x-2\right)^2}\)
Gọi hoành độ tiếp điểm là \(a\Rightarrow y=-\dfrac{4}{\left(a-2\right)^2}\left(x-a\right)+\dfrac{a+2}{a-2}\) là tiếp tuyến
\(x_A=2\Rightarrow y_A=-\dfrac{4}{\left(a-2\right)^2}\left(2-a\right)+\dfrac{a+2}{a-2}=\dfrac{a+6}{a-2}\) \(\Rightarrow A\left(2;\dfrac{a+6}{a-2}\right)\)
\(y_B=1\Rightarrow-\dfrac{4}{\left(a-2\right)^2}\left(x_A-a\right)+\dfrac{a+2}{a-2}=1\Rightarrow x_A=2a-2\) \(\Rightarrow B\left(2a-2;1\right)\)
\(\Rightarrow\overrightarrow{AB}=\left(2a-4;-\dfrac{8}{a-2}\right)\Rightarrow AB=\sqrt{4\left(a-2\right)^2+\dfrac{64}{\left(a-2\right)^2}}\)
\(AB=2\sqrt{\left(a-2\right)^2+\dfrac{16}{\left(a-2\right)^2}}\ge2\sqrt{2\sqrt{\dfrac{16\left(a-2\right)^2}{\left(a-2\right)^2}}}=4\sqrt{2}\)
\(\Rightarrow R=\dfrac{AB}{2}\ge2\sqrt{2}\)
\(\Rightarrow C=2\pi R\ge4\pi\sqrt{2}\)

Tập xác định D= R\{1}.
Đạo hàm 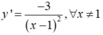
(C) có tiệm cận đứng x=1 (d1) và tiệm cận ngang y=2 (d2) nên I(1 ;2).
Gọi 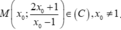 .
.
Tiếp tuyến ∆ của (C) tại M có phương trình
![]()
∆ cắt d1 tại 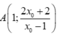 và cắt d2 tại
và cắt d2 tại ![]() .
.
Ta có 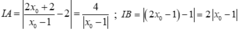 .
.
Do đó 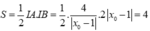 .
.
Chọn C.

Tập xác định D= R\ { 1}.
Đạo hàm y ' = - 3 ( x - 1 ) 2 , ∀ x ≠ 1 .
Đồ thị hàm số C có tiệm cận đứng là x= 1 và tiệm cận ngang y= 2 nên I (1 ;2 ) là giao của 2 đường tiệm cận.
Gọi M ( x 0 ; 2 x 0 + 1 x 0 - 1 ) ∈ ( C ) , x 0 ≠ 1 .
Tiếp tuyến ∆ của C tại M có phương trình là :
⇔ y = - 3 ( x 0 - 1 ) 2 ( x - x 0 ) + 2 x 0 + 1 x 0 - 1
∆ cắt TCĐ tại A ( 1 ; 2 x 0 + 2 x 0 - 1 ) và cắt TCN tại B( 2x0-1 ; 2) .
Ta có I A = 2 x 0 + 2 x 0 - 1 - 2 = 4 x 0 - 1 ; I B = ( 2 x 0 - 1 ) - 1 = 2 x 0 - 1 .
Do đó, S = 1 2 I A . I B = 1 2 4 x 0 - 1 . 2 x 0 - 1 = 4 .
Chọn D.

Chọn A
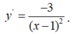
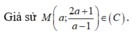
Phương trình tiếp tuyến tại điểm M là d: 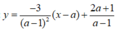
Đồ thị có hai tiệm cận có phương trình lần lượt là d 1 : x = 1; d 2 : y = 2
d cắt
d
1
tại điểm 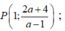
d cắt d 2 tại điểm Q(2a-1;2), d 1 cắt d 2 tại điểm I(1;2)
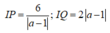
Ta có 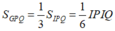
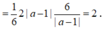



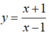

Vì tam giác IAB cân tại I nên tiếp tuyến phải song song với một trong 2 đường thẳng có phương trình \(y=x;y=-x\).
Ta có \(y'=\frac{1}{\left(x+2\right)^2}>0;x\ne-2\)
Mọi \(M\left(x_0;y_0\right)\) là tiếp điểm thì \(y'\left(x_0\right)=1\Leftrightarrow1=\frac{1}{\left(x_0+2\right)^2}\Leftrightarrow\left[\begin{array}{nghiempt}x_0=-1\\x_0=-3\end{array}\right.\)
Từ đó suy ra 2 tiếp tuyến là \(y=x+1;y=x+5\)