Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

phuong tring duong thang di qua 2 diem la do thi co dang y=ax+b
a,\(A\left(1;5\right)\in\) do thi nen ta co \(5=a+b\)
\(B\left(-2;-1\right)\) nen ta co \(-1=-2a+b\)
giai he pt ta co a=2, b=3 nen do thi co dang \(y=2x+3\)
b tuong tu ta co he \(\hept{\begin{cases}1=a+b\\-3=5a+b\end{cases}\Rightarrow a=-1,b=2}\)
do thi co dang \(y=-x+2\)

\(a,\) Gọi đt cần tìm là \(y=ax+b\)
\(\Leftrightarrow\left\{{}\begin{matrix}4a+b=-5\\a=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=3\end{matrix}\right.\Leftrightarrow y=-2x+3\)
\(b,\) Gọi đt cần tìm là \(y=ax+b\)
\(\Leftrightarrow\left\{{}\begin{matrix}8a+b=-1\\b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{1}{4}\\b=1\end{matrix}\right.\Leftrightarrow y=-\dfrac{1}{4}x+1\)
\(c,\) Gọi đt đi qua M và N là \(y=ax+b\)
\(\Leftrightarrow\left\{{}\begin{matrix}-2a+b=-3\\-6a+b=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=-2\end{matrix}\right.\Leftrightarrow y=\dfrac{1}{2}x-2\)
Thay \(x=1;y=1\Leftrightarrow1=\dfrac{1}{2}\cdot1-2\Leftrightarrow1=-\dfrac{1}{2}\left(\text{vô lí}\right)\)
\(\Leftrightarrow P\notinđths\)
Vậy 3 điểm này ko thẳng hàng

Gọi pt đường thẳng đi qua 2 điểm A và B là (d)y = ax + b ( a khác 0 )
Vì \(A\left(-1;-2\right)\in\left(d\right)\)\(\Rightarrow-2=-a+b\left(1\right)\)
Vì \(B\left(3;-10\right)\in\left(d\right)\Rightarrow-10=3a+b\left(2\right)\)
Lấy (1) trừ (2) theo từng vế được
\(-2-\left(-10\right)=-a+b-3a-b\)
\(\Leftrightarrow8=-4a\)
\(\Leftrightarrow a=-2\)
Thay vào (1) : \(-2=-\left(-2\right)+b\)
\(\Leftrightarrow2+b=-2\)
\(\Leftrightarrow b=-4\)
\(\Rightarrow\left(d\right)y=-2x-4\)
Vậy ......................
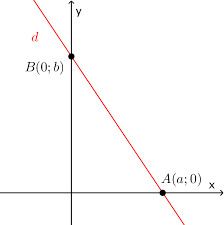
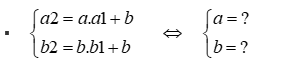
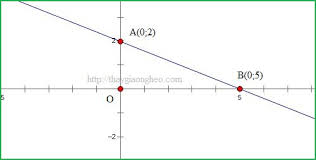
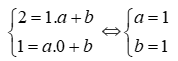
Phương trình đường thẳng có dạng \(\left(d\right):y=ax+b\)
a) \(A\left(0;-3\right)\cap B\left(1;-1\right)\in\left(d\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}a.0+b=-3\\a.1+b=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-3\\a=2\end{matrix}\right.\)
Vậy \(\left(d\right):y=2x-3\)
b) \(A\left(1;5\right)\cap B\left(-1;4\right)\in\left(d\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}a.1+b=5\\a.\left(-1\right)+b=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=5\\-a+b=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2b=9\\a+b=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=\dfrac{9}{2}\\a=5-\dfrac{9}{2}=\dfrac{1}{2}\end{matrix}\right.\)
Vậy \(\left(d\right):y=\dfrac{1}{2}x+\dfrac{9}{2}\)
Gọi (d): y = ax + b là phương trình đường thẳng cần viết
a) Do (d) đi qua A(0; -3)
⇒ b = -3
⇒ (d): y = ax - 3
Do (d) đi qua (1; -1)
⇒ a.1 - 3 = -1
⇔ a = -1 + 3
⇔ a = 2
⇒ (d): y = 2x - 3
b) Do (d) di qua A(1; 5)
⇒ a.1 + b = 5
⇔ a + b = 5
⇔ a = 5 - b (1)
Do (d) đi qua B(-1; 4)
⇒ a.(-1) + b = 4
⇔ b - a = 4 (2)
Thay (1) vào (2) ta có:
b - (5 - b) = 4
⇔ b - 5 + b = 4
⇔ 2b = 4 + 5
⇔ 2b = 9
⇔ b = 9/2
Thay b = 9/2 vào (1) ta có:
a = 5 - 9/2
⇔ a = 1/2
Vậy (d): y = x/2 + 9/2