Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

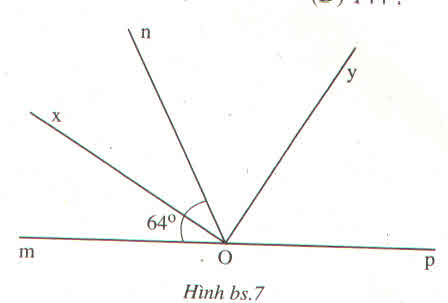
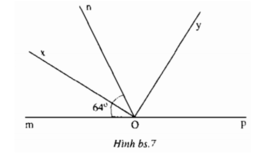
Có Ox là tia phân giác của góc mOn
mà góc mOn \(64^{^{ }0}\)
=>góc mOx = góc nOx = \(\dfrac{64^0}{2}=32^0\)
Có góc mOn + góc pOn = \(180^0\)(2 góc kề bù)
=> góc pOn = \(180^0\)- góc mOn
=> góc pOn = \(180^0-64^0=116^0\)
mà Oy là tia phân giác của góc pOn
=> góc pOy = góc nOy = \(\dfrac{116^0}{2}=58^0\)
Có tia On nằm giữa hai tia Ox và Oy
=> góc xOn + góc yOn = góc xOy
=> \(32^0+58^0\) = góc xOy
=> góc xOy = \(90^0\)
Vậy đáp án đúng là (A) \(90^0\)
*vì nỘp và nÔm kề bù
=> góc pOn+ nOm= 180 độ
=>góc pOn+64 độ = 180 độ
=> pOn= 116 độ
*vì Ox là tia phân giác của góc mOn
=>góc nOx= góc xOm= góc nOm/2= 64 độ/2= 32 độ
*vì Oy là tia phân giác của góc nOp
=>góc pOy= góc yOn=góc nOp/2= 116 độ/2= 58 độ
*góc xOy=góc yOn+ góc nOx
=> góc xOy =58 độ+ 32 độ
=>góc xOy = 90 độ
TA CHỌN CÂU (A.) 90 độ

Từ giả thiết ta vẽ được hình bs.15
Vì góc nOp kề bù với góc mOn suy ra góc mOp là góc bẹt.
Vì ∠(mOn) =30o và góc pOq phụ với góc mOn nên ∠(pOq) = 60o
Vì ∠(mOn) =30o và góc nOp kề bù với góc mOn nên ∠(nOp) = 150o
Do tia Oq nằm trong góc nOp nên ∠(nOp) = ∠(nOq) + ∠(qOp) hay ∠(nOq) + 60o = 150o. Từ đó (nOq) =90o.

a: \(\widehat{nOt}=120^0-90^0=30^0\)
b: \(\widehat{mOz}=120^0-90^0=30^0\)
b: \(\widehat{zOx}=60^0-30^0=30^0\)

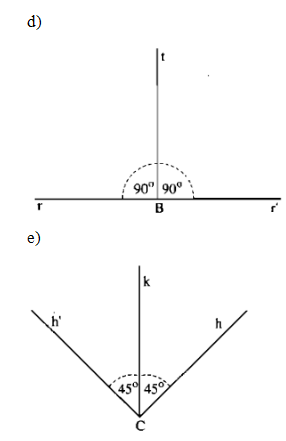
Bài tập dạng này có nhiều trường hợp về hình vẽ. Chỉ yêu cầu HS vẽ đúng một trường hợp, riêng với các ý c, d, và e chú ý có 2 trường hợp về hình vẽ:

Giải:
Có thể vẽ hình như sau:
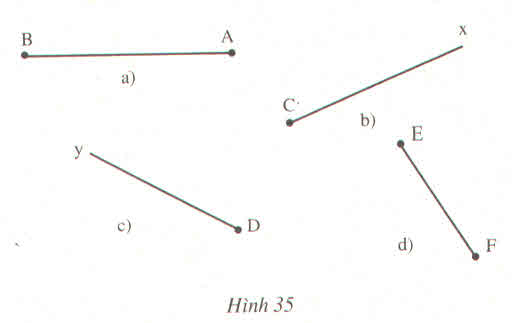
a) Đỉnh của góc là A, một cạnh là AB, cần vẽ tia AC.
b) Đỉnh của góc là C, một cạnh là Cx, cần vẽ tia Cz.
c) Đỉnh của góc là D, một cạnh là Dy, cần vẽ tia Dx.
d) Đỉnh của góc là F, Một cạnh là EF, cần vẽ tia Fy.

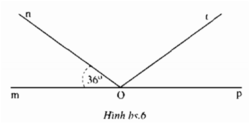

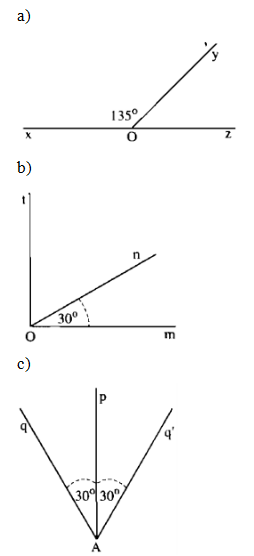
Có góc pOt phụ với góc mOn hay:
góc pOt + góc mOn = \(90^0\)
=> góc pOt = \(90^0\)- góc mOn
=> góc pOt = \(90^0-36^0\)
=> góc pOt = \(54^0\)
Có góc nOt + góc pOt + góc mOn = \(180^0\)
=> góc nOt = \(180^0\)- (góc pOt + góc mOt)
=> góc nOt = \(180^0-90^0\)
=> góc nOt = \(90^0\)
Vậy đáp án đúng là: (C) \(90^0\)