Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Trong hình 125a có 4 tam giác cân bằng nhau.
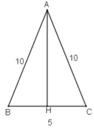
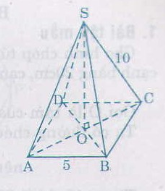
b) Gọi H là trung điểm BC. Tam giác ABC có AH là đường trung tuyến nên đồng thời là đường cao.
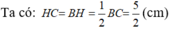
Chiều cao ứng với đáy của mỗi tam giác:
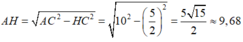
c) Chu vi đáy của hình chóp là 4.5 = 20 (cm).
Diện tích xung quanh hình chóp:
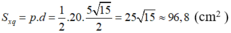
Diện tích đáy: Sd = 52 = 25 (cm2)
Diện tích toàn phần của hình chóp:
Stp = Sd + Sxq = 121,8 (cm2)

a) Trong hình 125a có 4 tam giác cân bằng nhau.
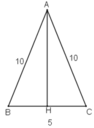
b) Gọi H là trung điểm BC. Tam giác ABC có AH là đường trung tuyến nên đồng thời là đường cao.
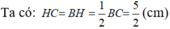
Chiều cao ứng với đáy của mỗi tam giác:
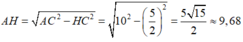
c) Chu vi đáy của hình chóp là 4.5 = 20 (cm).
Diện tích xung quanh hình chóp:
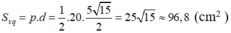
Diện tích đáy: Sd = 52 = 25 (cm2)
Diện tích toàn phần của hình chóp:
Stp = Sd + Sxq = 121,8 (cm2)

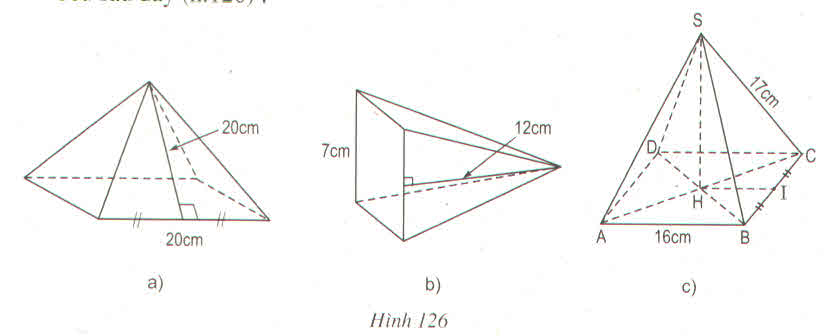
Hình a : Sxq = p.d = \(\dfrac{1}{2}\).20.4.20 = 800(cm2)
Diện tích đáy: Sđ = 202 = 400(cm2)
Diện tích toàn phần của lăng trụ hai là:
Stp = Sxq + Sđ = 800 + 400 = 1200(cm2)
Hình b: Sxq = p.d = \(\dfrac{1}{2}\).7.4.12 = 168(cm2)
Sđ = 72 = 49(cm2)
Stp = Sxq + Sđ = 168 + 49 = 217(cm2)
Hình c: Chiều cao của mặt bên của hình chóp:
\(h=\sqrt{17^2-8^2}=\sqrt{225}=15\left(cm\right)\)
Sxq = p.d = \(\dfrac{1}{2}\).16.4.15 = 480(cm2)
Sđ = 162 = 256(cm2)
Stp = Sxq + Sđ = 480 + 256 = 736(cm2)

a) Diện tích đáy của hình chóp đều:
S = BC 2 = 6,52 = 42,25 (m2)
Thể tích hình chóp đều:
V = \(\dfrac{1}{3}\). S.h = \(\dfrac{1}{3}\). 42,25 . 12 ≈ 169 (cm3)
b) Các mặt xung quanh là những hình thang cân đáy nhỏ 2cm, đáy lớn 4cm, chiều cao 3,5cm. Nên:
Sxq = \(4.\dfrac{\left(2+4\right).3,5}{2}=42\left(cm^2\right)\) = 42 (cm2)

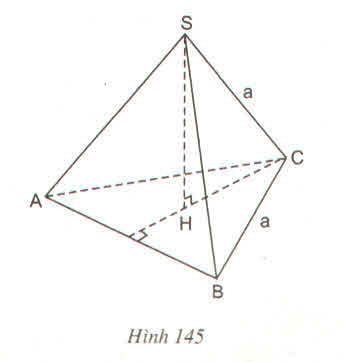
V = \(\dfrac{1}{3}\)S . h = \(\dfrac{1}{3}\)a.h.h = \(\dfrac{1}{3}\)ah2
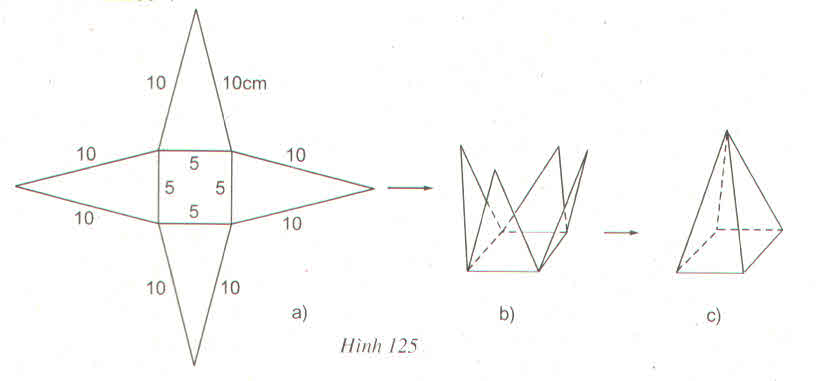


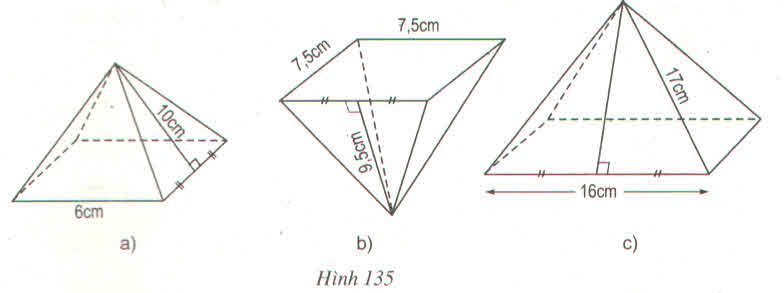
a) Trong hình 125a có 4 tam giác cân bằng nhau.
b) Chiều cao ứng với đáy của mỗi tam giác:
\(AH=\sqrt{AC^2-HC^2}\)
\(=\sqrt{AC^2-\left(\dfrac{1}{2}.5\right)^2}=\sqrt{100-\dfrac{25}{4}}=9,68\left(cm\right)\)
c) Diện tích xung quanh hình chóp:
Sxq = pd = \(\dfrac{1}{2}\).5.4.9,68 = 96,8 (cm2 )
Diện tích đáy:
Sđ = 52 = 25 (cm2 )
Diện tích toàn phần của hình chóp:
Stp = Sxq + Sđ = 121,8 (cm2 )