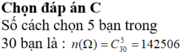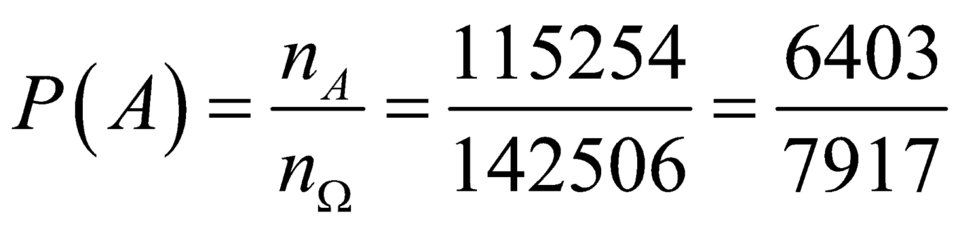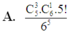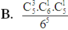Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Gọi A là biến cố “học sinh đăng ký Toán”
Gọi B là biến cố “học sinh đăng ký Lý”
![]() “học sinh đăng ký Toán, Lý”
“học sinh đăng ký Toán, Lý”
A u B là biến cố “học sinh có đăng ký học phụ đạo”
![]()
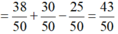
![]() là biến cố “học sinh không đăng ký môn nào cả”
là biến cố “học sinh không đăng ký môn nào cả”
![]()

Không gian mẫu : " Chọn 5 học sinh bất kì để đăng kí dự thi " là C530 cách

Đáp án A
Số phần tử của không gian mẫu là ![]()
Gọi A là biến cố“3 học sinh được chọn luôn có học sinh chọn môn Vật lý và học sinh chọn môn Hóa học”.
Số phần tử của biến cố A là
![]()
Vậy xác suất cần tìm là
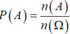
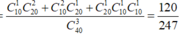

Chọn B
Số phần tử của không gian mẫu là ![]()
- Gọi A là biến cố “3 học sinh được chọn luôn có học sinh chọn môn Vật lý và học sinh chọn môn Hóa học”
- Số phần tử của biến cố A là
![]()
Vậy xác suất để xảy ra biến cố A là
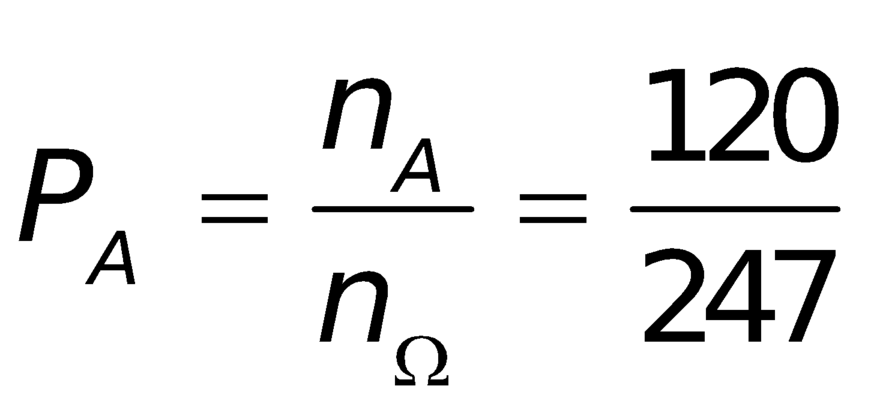 .
.

Đáp án B
Phương pháp giải: Áp dụng các quy tắm đếm cơ bản
Lời giải:
Một người có 6 cách chọn quầy khác nhau => Số phần tử của không gian mẫu là n ( Ω ) = 6 5
Chọn 3 học sinh trong 5 học sinh có C 5 3 cách, chọn 1 quầy trong 6 quầy có C 6 1 cách.
Suy ra có C 5 3 . C 6 1 cách chọn 3 học sinh vào 1 quầy bất kì.
Khi đó, 2 học sinh còn lại sẽ chọn 5 quầy còn lại => có C 5 1 cách.
Do đó, số kết quả thuận lợi cho biến cố là n ( X ) = C 5 1 . C 6 1 . C 5 1
Vậy P = n ( X ) n ( Ω ) = C 5 3 . C 6 1 . C 5 1 6 5