Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn:
+ Khi qua VTCB vật đạt vận tốc cực đại: \(v_{max}=\omega.A=62,8(cm/s)=20\pi(cm/s)\)
+ Khi vật ở biên thì gia tốc cực đại: \(a_{max}=\omega^2.A=200cm/s^2\)
Giải hệ pt trên ta tìm đc \(\omega=\pi(rad/s) \); \(A=20cm\)

Vận tốc của vật tại vị trí cân bằng v = vmax, gia tốc của vật tại biên a = amax.
Ta có
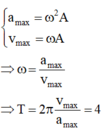
Đáp án C

Bạn xem lại giả thiết xem có thừa thiếu chỗ nào không nhé, giả thiết bài này khó hiểu quá.

1. Chu kì dao động: T = 4.0,2=0,8s
2. Chu kì T = 2.0,1 = 0,2s
3. \(a=-\omega^2.x\Rightarrow \omega=\sqrt{|\dfrac{a}{x}|}=\sqrt{\dfrac{80}{2}}=2\pi(rad/s)\)
\(\Rightarrow T = 1s\)

V = 50 cm/s = 0,5 m/s
Khi đi qua vị trí cân bằng thì :
Vmax = \(\omega A=0,5\frac{m}{s}\)(*)
Khi ở biên độ thì Amax = \(A\omega^2=5\frac{m}{s^2}\) (**)
Lấy (**) chia (*) => \(\omega=10\)
Vậy Amax /w = 0,05 m = 5 cm

Đáp án B
+ Phát biểu đúng là:
(e) cứ mỗi chu kỳ dao động, có 4 thời điểm thế năng và động năng của vật bằng nhau.
(g) gia tốc đạt giá trị cực tiểu khi vật ở ly độ cực đại.
+ Khi qua VTCB, vận tốc đạt cực đại \(\Rightarrow v_{max}=\omega A = 1 \ (cm/s)\) (1)
+ Khi ở biên, gia tốc đạt cực đại \(\Rightarrow a_{max}=\omega^2 A = 1,57 \ (cm/s^2)\) (2)
Từ (1) và (2): \(\omega = 1,57 = \frac{\pi}{2} \ (rad/s)\)
Vậy chu kì: T = 4s
tìm A kiểu j vậy