Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ các công thức (13.5), (13.6) và (13.7), ta có:
\(U_{AB}=V_A-V_B=\dfrac{A_{A\infty}}{q}-\dfrac{A_{B\infty}}{q}=\dfrac{A_{A\infty}-A_{B\infty}}{q}\)
Mà: \(A_{A\infty}=A_{AB}+A_{B\infty}\)
\(\Rightarrow U_{AB}=\dfrac{A_{AB}+A_{B\infty}-B_{B\infty}}{q}=\dfrac{A_{AB}}{q}\)

Độ biến thiên động năng bằng công của lực điện trường:
\({W_d} - {W_{d0}} = A \Rightarrow \frac{1}{2}m{v^2} - 0 = {q_e}Ed \Rightarrow v = \sqrt {\frac{{2{q_e}Ed}}{m}} \)

Ta có:
\(W_t=\dfrac{1}{2}m\omega^2A^2cos^2\left(\omega t+\varphi_0\right)\\ W_d=\dfrac{1}{2}mv^2=\dfrac{1}{2}m\omega^2A^2sin^2\left(\omega t+\varphi_0\right)\\ \Rightarrow W=W_t+W_d=\dfrac{1}{2}m\omega^2A^2\left[cos^2\left(\omega t+\varphi_0\right)+sin^2\left(\omega t+\varphi_0\right)\right]\\ \Rightarrow W=\dfrac{1}{2}m\omega^2A^2\)

Hiệu điện thế UMN bằng độ biến thiên thế năng từ M đến N: UMN = VM - VN
\({V_{MN}} = \frac{{{A_{MN}}}}{q}\) ⇒ ANM = (VM−VN)q = UMN.q

Công thức (3.5): \(W_d=\dfrac{1}{2}mw^2A^2sin^2\left(wt+\varphi_0\right)\)
Đồ thị động năng – thời gian cũng có dạng hình sin.
Từ đồ thị ta thấy:
+ Tại thời điểm ban đầu, động năng bằng 0
+ Tại thời điểm \(\dfrac{T}{4}\), động năng cực đại
+ Tại thời điểm \(\dfrac{T}{2}\), động năng bằng 0
+ Tại thời điểm \(\dfrac{3T}{4}\), động năng cực đại
+ Tại thời điểm T, động năng bằng 0.

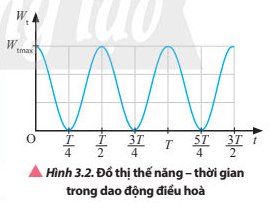
Thế năng của vật đạt giá trị lớn khi ở vị trí hai biên và đạt giá trị nhỏ nhất ở vị trí cân bằng khi vật di chuyển từ vị trí biên đến vị trí cân bằng thế năng của vật giảm dần từ giá trị lớn nhất về 0 và ngược lại.

Tần số sóng trên dây càng lớn, số bụng sóng càng nhiều. Số bụng sóng tỉ lệ với tần số sóng.


Ta có: \(A=\dfrac{1}{2}QU\)
Công tổng cộng để tích điện cho tụ từ trạng thái ban đầu đến khi có điện tích Q là năng lượng được dự trữ trong tụ điện dưới dạng năng lượng điện trường.
Và Q=CU nên thay vào công thức trên ta thu được:
\(W=\dfrac{1}{2}QU=\dfrac{1}{2}CU^2=\dfrac{Q^2}{2C}\)