
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\frac{2002}{2001}+\frac{2003}{2002}+\frac{2004}{2003}+\frac{2005}{2004}+\frac{2006}{2005}+\frac{2007}{2006}+\frac{2008}{2007}+\frac{2009}{2008}>\frac{2001}{2001}+\frac{2002}{2002}+\frac{2003}{2003}+\frac{2004}{2004}+\frac{2005}{2005}+\frac{2006}{2006}+\frac{2007}{2007}+\frac{2008}{2008}\)
\(A=\frac{2002}{2001}+\frac{2003}{2002}+\frac{2004}{2003}+\frac{2005}{2004}+\frac{2006}{2005}+\frac{2007}{2006}+\frac{2008}{2007}+\frac{2009}{2008}>1+1+1+1+1+1+1+1\)\(A=\frac{2002}{2001}+\frac{2003}{2002}+\frac{2004}{2003}+\frac{2005}{2004}+\frac{2006}{2005}+\frac{2007}{2006}+\frac{2008}{2007}+\frac{2009}{2008}>8\)
\(A>8\)



a) Điền từ trái sang phải:
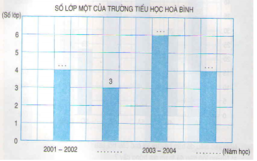
- Các đỉnh cột: 4, 6, 4
- Các chân cột: 2002 – 2003, 2004 – 2005
b) - Số học sinh lớp Một của năm học 2003- 2004 nhiều hơn của năm học 2002 - 2003 là:
6 - 3 = 3 lớp
- Số học sinh lớp Một trong năm học 2002 - 2003 của trường tiều học Hòa Bình là:
35 x 3 = 105 học sinh
- Số học sinh lớp Một trong năm học 2004 - 2005 của trường tiều học Hòa Bình là:
32 x 4 = 128 học sinh
- Số học sinh lớp Một năm hoc 2002 - 2003 ít hơn của năm học 2004- 2005 là :
128 - 105 = 23 học sinh

a) Điền từ trái sang phải:
- Các đỉnh cột: 4, 6, 4
- Các chân cột: 2002 – 2003, 2004 – 2005
b) - Số học sinh lớp Một của năm học 2003- 2004 nhiều hơn của năm học 2002 - 2003 là:
6 - 3 = 3 lớp
- Số học sinh lớp Một trong năm học 2002 - 2003 của trường tiều học Hòa Bình là:
35 x 3 = 105 học sinh
- Số học sinh lớp Một trong năm học 2004 - 2005 của trường tiều học Hòa Bình là:
32 x 4 = 128 học sinh
- Số học sinh lớp Một năm hoc 2002 - 2003 ít hơn của năm học 2004- 2005 là :
128 - 105 = 23 học sinh



a) \(\frac{2005.2007-1}{2004+2005.2006}=\frac{\left(2014+1\right).2007-1}{2004+2005.2006}=\frac{2004+2005.2007-1}{2004+2005-2006}=\frac{2004+2005.2006}{2004+2005.2006}=1\)

\(\frac{2003}{2004}+\frac{2004}{2005}+\frac{2005}{2003}=1-\frac{1}{2004}+1-\frac{1}{2005}+1+\frac{2}{2003}\)
\(=3+\left(\frac{1}{2003}-\frac{1}{2004}\right)+\left(\frac{1}{2003}-\frac{1}{2005}\right)\)
Do \(\frac{1}{2003}>\frac{1}{2004}>\frac{1}{2005}.\) nên \(\left(\frac{1}{2003}-\frac{1}{2004}\right)+\left(\frac{1}{2003}-\frac{1}{2005}\right)>0\)
Vì vậy \(3+\left(\frac{1}{2003}-\frac{1}{2004}\right)+\left(\frac{1}{2003}-\frac{1}{2005}\right)>3\) (đpcm)
\(A=\frac{2003}{2004}+\frac{2004}{2005}+\frac{2005}{2003}\)
\(=(1-\frac{1}{2004})+(1-\frac{1}{2005})+(1+\frac{2}{2003})\)
\(=3+(\frac{1}{2003}+\frac{1}{2003}-\frac{1}{2004}-\frac{1}{2005})\)
Do\(\frac{1}{2003}\)>\(\frac{1}{2004}\)>\(\frac{1}{2005}\)
\(\Rightarrow\frac{1}{2003}+\frac{1}{2003}+\frac{1}{2004}+\frac{1}{2005}\)>\(0\)
\(\Rightarrow3+(\frac{1}{2003}-\frac{1}{2004}+\frac{1}{2003}-\frac{1}{2005})\)>\(3\)
\(\Rightarrow A\)>\(3\)

Ta có:\(\frac{2003.2004-2001}{2002.2003+2005}=\frac{\left(2002+1\right).2004-2001}{2002.\left(2004-1\right)+2005}\)
=\(\frac{2002.2004+2004-2001}{2002.2004-2002+2005}\)
=\(\frac{2002.2004+3}{2002.2004+2005-2002}\)
=\(\frac{2002.2004+3}{2002.2004+3}\)=1
Vay\(\frac{2003.2004-2001}{2002.2003+2005}=1\)