Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\) ( k # 0 )
\(\Rightarrow\) \(a=b.k\)
\(c=d.k\)
Ta có: \(\dfrac{a+b}{b}=\dfrac{b.k+b}{b}=\dfrac{b.\left(k+1\right)}{b}=k+1\) (1)
\(\dfrac{c+d}{d}=\dfrac{d.k+d}{d}=\dfrac{d.\left(k+1\right)}{d}=k+1\) (2)
Từ (1) và (2) \(\Rightarrow\) \(\dfrac{a+b}{b}=\dfrac{c+d}{d}\)
b,
, Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\) ( k # 0 )
\(\Rightarrow\) \(a=b.k\)
\(c=d.k\)
Ta có: \(\dfrac{a}{a+b}=\dfrac{b.k}{b.k+b}=\dfrac{b.k}{b.\left(k+1\right)}=\dfrac{k}{k+1}\) (1)
\(\dfrac{c}{c+d}=\dfrac{d.k}{d.k+d}=\dfrac{d.k}{d.\left(k+1\right)}=\dfrac{k}{k+1}\) (2)
Từ (1) và (2) \(\Rightarrow\) \(\dfrac{a}{a+b}=\dfrac{c}{c+d}\)

Xét: \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
\(\Rightarrow a=bk;c=dk\) (1)
Thay (1) vào \(\dfrac{a+c}{a-c}=\dfrac{b+d}{b-d}\)
\(=\dfrac{bk+dk}{bk-dk}=\dfrac{b+d}{b-d}\)
\(=\dfrac{k\left(b+d\right)}{k\left(b-d\right)}=\dfrac{b+d}{b-d}\)
\(\dfrac{b+d}{b-d}=\dfrac{b+d}{b-d}\)
Vậy \(\dfrac{a}{b}=\dfrac{c}{d}\) thì \(\dfrac{a+c}{a-c}=\dfrac{b+d}{b-d}\) (đpcm)

b,
\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{b}{d}=\dfrac{a}{c}=\dfrac{b+a}{d+c}\\ \Rightarrow\dfrac{a}{a+b}=\dfrac{c}{c+d}\)
c,
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
ta có: \(a=bk;c=dk\)
\(\Rightarrow\dfrac{2a+3c}{2b+3d}=\dfrac{2bk+3dk}{2b+3d}=\dfrac{k^2.\left(2b+3d\right)}{2b+3d}=k^2\\ \Rightarrow\dfrac{2a-3c}{2b-3d}=\dfrac{2bk-3dk}{2b-3d}=\dfrac{k^2.\left(2b-3d\right)}{2b-3d}=k^2\\ \Rightarrow\dfrac{2a+3c}{2b+3d}=\dfrac{2a-3c}{2b-3d}\)
d,
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
ta có:\(a=bk;c=dk\)
\(\Rightarrow\dfrac{ac}{bd}=\dfrac{bk.dk}{bd}=k^2\\ \Rightarrow\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{k^2.\left(b+d\right)^2}{\left(b+d\right)^2}=k^2\\ \Rightarrow\dfrac{ac}{bd}=\dfrac{a^2+c^2}{b^2+d^2}\)
e,
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
Ta có:\(a=bk;c=dk\)
\(\Rightarrow\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{k^2.\left(b+d\right)^2}{\left(b+d\right)^2}=k^2\\ \Rightarrow\dfrac{a^2-c^2}{b^2-d^2}=\dfrac{k^2.\left(b-d\right)^2}{\left(b-d\right)^2}=k^2\\ \Rightarrow\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{a^2-c^2}{b^2-d^2}\)
f,
(để hôm sau lm nha, mỏi tay quá)
a, \(\dfrac{a}{b}\)=\(\dfrac{c}{d}\)=> \(\dfrac{a}{c}\)=\(\dfrac{b}{d}\)=\(\dfrac{a+b}{c+d}\)=\(\dfrac{a-b}{c-d}\)(1)
\(\dfrac{a+b}{c+d}\)=\(\dfrac{a-b}{c-d}\)=> \(\dfrac{a+b}{a-b}\)=\(\dfrac{c+d}{c-d}\)
Còn các phần còn lại làm giống thế

Giải:
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{a+c}{b+d}=\dfrac{a-c}{b-d}\)
\(\Rightarrow\dfrac{a+c}{b+d}=\dfrac{a-c}{b-d}\)
\(\Rightarrow\dfrac{a+c}{a-c}=\dfrac{b+d}{b-d}\left(đpcm\right)\)
Vậy...
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{a+c}{b+d}=\dfrac{a-c}{b-d}\)
Từ đó suy ra : \(\dfrac{a+c}{a-c}=\dfrac{b+d}{b-d}\)

C) đúng. Vì
\(\dfrac{a}{b}=\dfrac{c}{d}\)
=>\(\dfrac{a}{c}=\dfrac{b}{d}\)
=>\(\dfrac{c}{a}=\dfrac{d}{b}\)

Giải:
Ta có: \(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}\)
\(\Rightarrow\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}\Rightarrow\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\left(đpcm\right)\)
Vậy...
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
=>\(\left\{{}\begin{matrix}a=b.k\\c=d.k\end{matrix}\right.\) (1)
Thay (1) vào:
\(\dfrac{a+b}{a-b}=\dfrac{b.k+b}{b.k-b}=\dfrac{b.\left(k+1\right)}{b.\left(k-1\right)}=\dfrac{k+1}{k-1}\) (2)
\(\dfrac{c+d}{c-d}=\dfrac{d.k+d}{d.k-d}=\dfrac{d.\left(k+1\right)}{d.\left(k-1\right)}=\dfrac{k+1}{k-1}\) (3)
Từ (2) và (3) =>\(\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}=\dfrac{k+1}{k-1}\)

Ta có : \(\dfrac{a}{b}=\dfrac{c}{d}\) suy ra \(\dfrac{a}{c}=\dfrac{b}{d}\)
Theo tính chất dãy tỉ số bằng nhau ta có
\(\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}\)
Suy ra: \(\dfrac{a+b}{a-c}=\dfrac{c+d}{c-d}\)
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
\(\Rightarrow a=bk\) và \(c=dk\)
Nên \(\dfrac{a+b}{c-d}=\dfrac{bk+b}{dk-d}=\dfrac{b\left(k+1\right)}{d\left(k-1\right)}=\dfrac{k+1}{k-1}\)
\(\dfrac{c+d}{c-d}=\dfrac{dk+d}{dk-d}=\dfrac{d\left(k+1\right)}{d\left(k-1\right)}=\dfrac{k+1}{k-1}\)
\(\Rightarrow\dfrac{a+b}{c-d}=\dfrac{c+d}{c-d}\) (với \(a-b\ne0,c-d\ne0\))
Vậy \(\dfrac{a}{b}=\dfrac{c}{d}thì\)\(\dfrac{a+b}{c-d}=\dfrac{c+d}{c-d}\) ( \(a-b\ne0,c-d\ne0\))

Ta có : \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
=> a = b.k ; c = d.k
Ta lại có : \(\dfrac{a-b}{a+b}=\dfrac{b.k-b}{b.k+b}=\dfrac{b.\left(k-1\right)}{b.\left(k+1\right)}=\dfrac{k-1}{k+1}\)
\(\dfrac{c-d}{c+d}=\dfrac{d.k-d}{d.k+d}=\dfrac{d.\left(k-1\right)}{d.\left(k+1\right)}=\dfrac{k-1}{k+1}\)
Vì \(\dfrac{a-b}{a+b}=\dfrac{k-1}{k+1}\) ; \(\dfrac{c-d}{c+d}=\dfrac{k-1}{k+1}\) nên \(\dfrac{a-b}{a+b}=\dfrac{c-d}{c+d}\)
Vậy \(\dfrac{a-b}{a+b}=\dfrac{c-d}{c+d}\)

Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\) thì \(a=b.k\) , \(c=d.k\)
Ta tính giá trị của các tỉ số \(\dfrac{a-b}{a};\dfrac{c-d}{c}\) theo \(k\)
\(\dfrac{a-b}{a}=\dfrac{b.k-b}{b.k}=\dfrac{b.\left(k-1\right)}{b.k}=\dfrac{k-1}{k}\left(1\right)\)
\(\dfrac{c-d}{c}=\dfrac{d.k-d}{d.k}=\dfrac{d\left(k-1\right)}{d.k}=\dfrac{k-1}{k}\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\) suy ra \(\dfrac{a-b}{a}=\dfrac{c-d}{c}\)
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow\left\{{}\begin{matrix}a=bk\\b=ck\end{matrix}\right.\)
Ta có : \(\dfrac{a-b}{a}=\dfrac{bk-b}{bk}=\dfrac{b\left(k-1\right)}{k}=\dfrac{k-1}{k}\left(1\right)\)
\(\dfrac{c-d}{c}=\dfrac{dk-d}{dk}=\dfrac{d\left(k-1\right)}{dk}=\dfrac{k-1}{k}\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) suy ra : \(\dfrac{a-b}{a}=k=\dfrac{c-d}{c}\)
\(\Rightarrow\dfrac{a-b}{a}=\dfrac{c-d}{c}\left(ĐPCM\right)\)
Vậy \(\dfrac{a-b}{a}=\dfrac{c-d}{c}\)
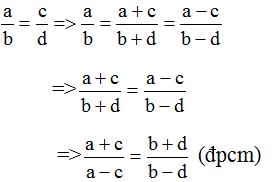
Đặt: \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
Lần lượt thay a và c vào các ý cần chứng minh, áp dụng theo tính chất phân phối giữa phép nhân đối với phép cộng (hay phép trừ) để tính ở mỗi vế.
Mẫu: a) Ta có : \(\dfrac{a+b}{b}=\dfrac{bk+b}{b}=\dfrac{b\left(k+1\right)}{b}=k+1\)
\(\dfrac{c+d}{d}=\dfrac{dk+d}{d}=\dfrac{d\left(k+1\right)}{d}=k+1\)
\(\Rightarrow\dfrac{a+b}{b}=\dfrac{c+d}{d}\)
Vậy \(\dfrac{a+b}{b}=\dfrac{c+d}{d}\)
a)\(\dfrac{a+b}{b}=\dfrac{c+d}{d}\)
Gọi\(\dfrac{a}{b}=\dfrac{c}{d}=k\)
\(a=b.k\)
\(c=d.k\)
\(\dfrac{a+b}{b}=\dfrac{bk+b}{b}=\dfrac{b.\left(k+1\right)}{b}=k+1\) (1)
\(\dfrac{c+d}{d}=\dfrac{dk+d}{d}=\dfrac{d.\left(k+1\right)}{d}=k+1\)(2)
Từ (1) và (2) \(\Rightarrow\)\(\dfrac{a+b}{b}=\dfrac{c+d}{d}\)
b)\(\dfrac{a-b}{b}=\dfrac{c-d}{d}\)
Gọi\(\dfrac{a}{b}=\dfrac{c}{d}=k\)
\(a=b.k\)
\(c=d.k\)\(\dfrac{a-b}{a}=1-\dfrac{b}{a}=1-\dfrac{b}{bk}=1-\dfrac{1}{k}\left(1\right)\)
\(\dfrac{c-d}{c}=1-\dfrac{d}{c}=1-\dfrac{d}{dk}=1-\dfrac{1}{k}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\)\(\dfrac{a-b}{b}=\dfrac{c-d}{d}\)