Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C O D E N P
Xét đường tròn (O) có 2 tiếp tuyến NE, NC (E và C là tiếp điểm) => EN = CN (T/c 2 tiếp tuyến giao nhau)
Ta thấy: ^BAC nội tiếp (O), phân giác ^BAC cắt (O) tại điểm thứ hai E => E là điểm chính giữa cung nhỏ BC
=> OE vuông góc với BC. Mà EN vuông góc OE nên EN // BC. Áp dụng ĐL Thales có:
\(\frac{CN}{CD}=\frac{EN}{CD}=\frac{PN}{CP}\)=> \(\frac{CN}{CD}+\frac{CN}{CP}=\frac{PN+CN}{CP}=1\)=> \(\frac{1}{CN}=\frac{1}{CD}+\frac{1}{CP}\)(đpcm).

Em ko giải được nhưng anh có thể kết bạn với em không?

a) Vì AE là phân giác \(\widehat{BAC}\)
\(\Rightarrow\) \(\widehat{BAE}=\widehat{EAC}\) hay \(\widehat{BAD}=\widehat{EAC}\)
Xét (O) có: \(\widehat{CBA}=\widehat{AEC}\)(cùng chắn \(\stackrel\frown{AC}\))
hay \(\widehat{DBA}=\widehat{AEC}\)
Xét ΔBAD và ΔEAC có:
\(\widehat{BAD}=\widehat{EAC}\) (cmtrn)
\(\widehat{DBA}=\widehat{AEC}\) (cmtrn)
\(\Rightarrow\) ΔBAD∼ΔEAC (g.g)
\(\Rightarrow\frac{AB}{AD}=\frac{AE}{AC}\) \(\Leftrightarrow AB.AC=AE.AD\) (đpcm)
b) Theo CM a) ΔBAD∼ΔEAC
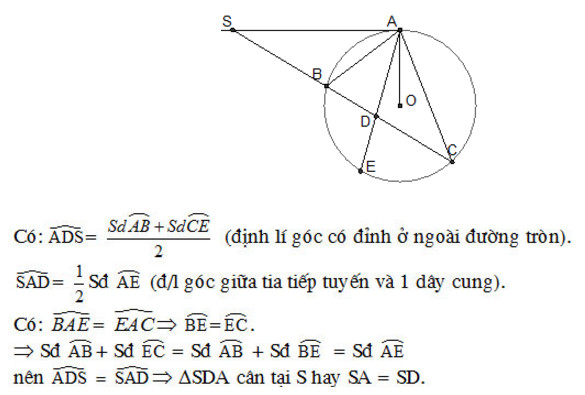
\(\widehat{BDA}=\widehat{ECA}\) hay \(\widehat{SDA}=\widehat{ECA}\) (1)
Xét (O) có: \(\widehat{ECA}=\widehat{EAS}\) (cùng chắn \(\stackrel\frown{EA}\))
hay \(\widehat{ECA}=\widehat{DAS}\) (2)
Từ (1) và (2) \(\Rightarrow\) \(\widehat{SDA}=\widehat{DAS} \) \((=\widehat{ECA})\)
\(\Rightarrow\) ΔDSA cân tại S
c) Xét (O) có: \(\widehat{BCA}=\widehat{BAS}\) (cùng chắn \(\stackrel\frown{AB}\))
hay \(\widehat{SCA}=\widehat{BAS}\)
Xét ΔCSA và ΔASB có:
\(\widehat{CSA}:chung\)
\(\widehat{SCA}=\widehat{BAS}\)
\(\Rightarrow\) ΔCSA∼ΔASB (g.g)
\(\Rightarrow\frac{SC}{SA}=\frac{SA}{SB}\) \(\Leftrightarrow SC.SB=SA^2\) (đpcm)
d) Xét (O) có: \(\widehat{ECP}=\widehat{EAC}\) (cùng chắn \(\stackrel\frown{EC}\))
hay \(\widehat{QCP}=\widehat{EAC}\) (3)
Theo CM a) \(\widehat{BAE}=\widehat{EAC}\) hay \(\widehat{QAP}=\widehat{EAC}\) (4)
Từ (3) và (4) \(\Rightarrow\) \(\widehat{QCP}=\widehat{QAP}\) \((=\widehat{EAC})\)
\(\Rightarrow\) Tứ giác QACP nội tiếp đường tròn (theo dhnb tứ giác nội tiếp).

giúp mik câu C đi