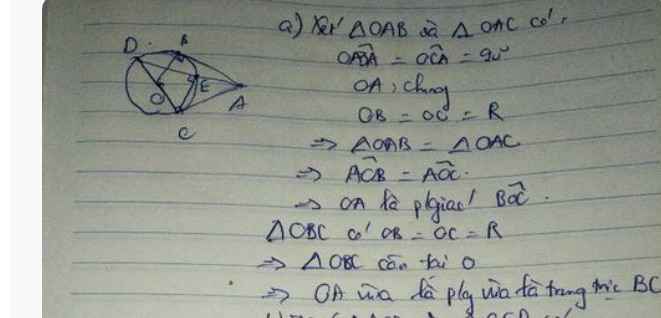Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

 I C B D O E
.Ta có :ICIC là tiếp tuyến của (O)
\(\Rightarrow\widehat{CIE}=\widehat{IBC}\)
\(\Rightarrow\)ΔICE∼ΔIBC(g.g)\(\Rightarrow\)
IEIC=ICIB→ICE^=IBC^→ΔICE∼ΔIBC(g.g)→IEIC=ICIB
\(\Rightarrow\)IC2=IE.IB→IC2=IE.IB
Ta có : BD//AC\(\Rightarrow\widehat{IAE}=\widehat{EDB}=\widehat{ABE}\)
\(\Rightarrow\)ΔAIE∼ΔBIA(g.g)\(\Rightarrow\)
AIBI=IEIA\(\Rightarrow\)
IA2=IB.IE→ΔAIE∼ΔBIA(g.g)→AIBI=IEIA→IA2=IB.IE
→IA2=IC2→IA=IC→I→IA2=IC2→IA=IC→I là trung điểm AC
Dễ có IC là tiếp tuyến của đường tròn nên IC2 = IB.IE (1)
Theo tính chất của góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung, ta có: ^EBA = ^BDA
Lại có: ^BDA = ^DAC (BD//AC, hai góc so le trong)
Từ đó suy ra ^EBA = ^DAC
∆AIE và ∆BIA có: ^AIB là góc chung, ^EBA = ^DAC (cmt) nên ∆AIE ~ ∆BIA (g.g)
=>\(\frac{IA}{IE}=\frac{IB}{IA}\Rightarrow IA^2=IB.IE\)(2)
Từ (1) và (2) suy ra IA2 = IC2 hay IA = IC
Vậy I là trung điểm của AC (đpcm)

a: ΔODE cân tại O có OI là trung tuyến
nên OI vuông góc DE
góc OIA+góc OBA=180 độ
=>OIAB nội tiếp
b: Xét ΔKCE và ΔKBC có
góc KCE=góc KBC
góc K chung
=>ΔKCE đồng dạng với ΔKBC
=>KC/KB=KE/KC
=>KC^2=KB*KE

a: Xét (O) có
AB,AC là tiếp tuyến
nên AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA vuông góc với BC
Xét tứ giác OBAC có
góc OBA+góc OCA=180 độ
nên OBAC là tứ giác nội tiếp
b: Xét ΔABE và ΔADB có
góc ABE=góc ADB
góc BAE chung
Do đó: ΔABE đồng dạng với ΔADB
=>AB/AD=AE/AB
=>AB^2=AD*AE=AH*AO