Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
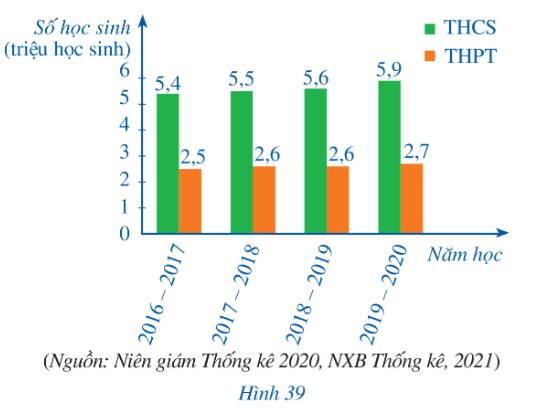
Năm học | 2016 - 2017 | 2017 - 2018 | 2018 - 2019 | 2019 – 2020 |
Số học sinh THCS | 5,4 | 5,5 | 5,6 | 5,9 |
Số học sinh THPT | 2,5 | 2,6 | 2,6 | 2,7 |
b)
Tỉ số của số học sinh THCS và số học sinh THPT trong năm 2016 – 2017 là: \(\frac{{5,4}}{{2,5}} \approx 2,2\)
Tỉ số của số học sinh THCS và số học sinh THPT trong năm 2017 – 2018 là: \(\frac{{5,5}}{{2,6}} \approx 2,1\)
Tỉ số của số học sinh THCS và số học sinh THPT trong năm 2018 – 2019 là: \(\frac{{5,6}}{{2,6}} \approx 2,2\)
Tỉ số của số học sinh THCS và số học sinh THPT trong năm 2019 – 2020 là: \(\frac{{5,9}}{{2,7}} \approx 2,2\)
Ta có bảng:
Năm học | 2016 - 2017 | 2017 - 2018 | 2018 - 2019 | 2019 – 2020 |
Tỉ số của số học sinh THCS và số học sinh THPT | 2,2 | 2,1 | 2,2 | 2,2 |
c) Trong Bảng 1, ta thấy rằng tỉ số của số học sinh THCS và số học sinh THPT qua các năm học gần như là không thay đổi. Điều này cho thấy số lượng học sinh tham gia học THCS và THPT trong các năm khá ổn định, không có quá nhiều sự biến đổi.

a)
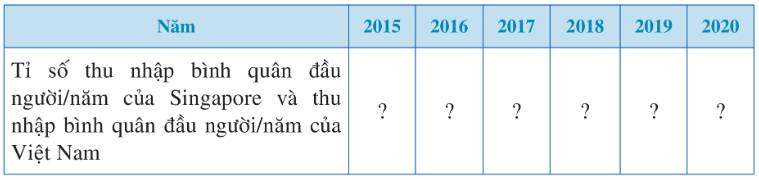
Tỉ số thu nhập bình quân đầu người/năm của Singapore và Việt Nam năm 2015 là: \(\frac{{55647}}{{2097}} \approx 26,5\)
Tỉ số thu nhập bình quân đầu người/năm của Singapore và Việt Nam năm 2016 là: \(\frac{{56848}}{{2202}} \approx 25,8\)
Tỉ số thu nhập bình quân đầu người/năm của Singapore và Việt Nam năm 2017 là: \(\frac{{61176}}{{2373}} \approx 25,8\)
Tỉ số thu nhập bình quân đầu người/năm của Singapore và Việt Nam năm 2018 là: \(\frac{{66679}}{{2570}} \approx 25,9\)
Tỉ số thu nhập bình quân đầu người/năm của Singapore và Việt Nam năm 2019 là: \(\frac{{65233}}{{2714}} \approx 24,0\)
Tỉ số thu nhập bình quân đầu người/năm của Singapore và Việt Nam năm 2020 là:
\(\frac{{59798}}{{2779}} \approx 21,5\)

b) Dựa vào bảng thống kê ta thấy từ năm 2015 đến năm 2017, tỉ số giảm dần. Từ năm 2017 đến năm 2018, tỉ số tăng. Từ năm 2018 đến năm 2020, tỉ số giảm nhanh.

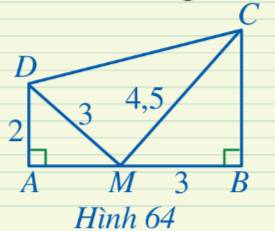
Vì \(\frac{{AD}}{{BM}} = \frac{2}{3},\,\,\frac{{DM}}{{MC}} = \frac{3}{{4,5}} = \frac{2}{3}\) nên \(\frac{{AD}}{{BM}} = \frac{{DM}}{{MC}}\).
Xét hai tam giác \(ADM\) và \(BMC\) có \(\widehat {MAD} = \widehat {CBM} = 90^\circ \) và \(\frac{{AD}}{{BM}} = \frac{{DM}}{{MC}}\) nên \(\Delta{ADM} \backsim \Delta{BMC}\).
Suy ra \(\widehat {AMD} = \widehat {BCM}\) và \(\widehat {ADM} = \widehat {BMC}\).
Xét tam giác \(ADM\) vuông tại A có:
\(\begin{array}{l}\,\,\,\,\,\,\,\,\widehat {AMD} + \widehat {ADM} = 90^\circ \\ \Rightarrow \widehat {AMD} + \widehat {BMC} = 90^\circ \end{array}\)
Mà ta có:
\(\begin{array}{l}\,\,\,\,\,\widehat {AMD} + \widehat {DMC} + \widehat {CMB} = 180^\circ \\ \Rightarrow 90^\circ + \widehat {DMC} = 180^\circ \\ \Rightarrow \widehat {DMC} = 90^\circ \end{array}\)
Vậy tam giác \(CDM\) vuông tại \(M\).

\({x^6} + {y^6} = {\left( {{x^2}} \right)^3} + {\left( {{y^2}} \right)^3} = \left( {{x^2} + {y^2}} \right)\left[ {{{\left( {{x^2}} \right)}^2} - {x^2}.{y^2} + {{\left( {{y^2}} \right)}^2}} \right] = \left( {{x^2} + {y^2}} \right)\left( {{x^4} - {x^2}{y^2} + {y^4}} \right)\)

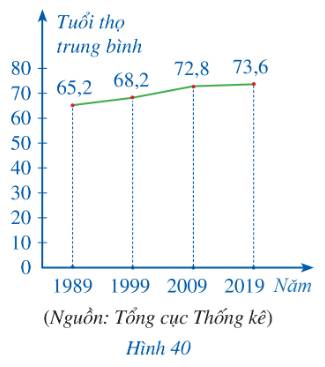
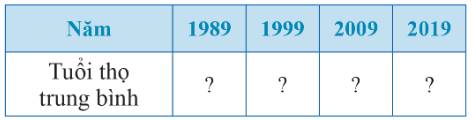
a) Ta có bảng:
Năm | 1989 | 1999 | 2009 | 2019 |
Tuổi thọ trung bình | 65,2 | 68,2 | 72,8 | 73,6 |
b) Tỉ số phần trăm giữa tuổi thọ trung bình của người Việt Năm năm 2019 so với năm 1989 là:
\(\frac{{73,6.100}}{{65,2}}\% \approx 113\% \)
Tuổi thọ trung bình của người Việt Năm năm 2019 so với năm 1989 đã tăng số % là:
\(113\% - 100\% = 13\% \)
Vậy thông tin của bài báo là không chính xác.

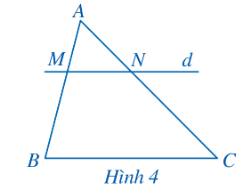
Xét tam giác ABC với \(MN\parallel BC\), ta có \(\frac{{MB}}{{AB}} = \frac{{NC}}{{AC}}\) (định lý Thales).

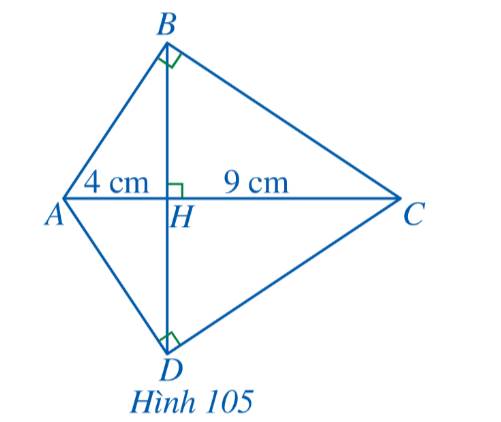
a) Xét tam giác ABC vuông tại B có: \(\widehat {BAC} + \widehat {BCA} = 90^\circ \)
Xét tam giác BHC vuông tại H có:
\(\begin{array}{l}\widehat {HBC} + \widehat {HCB} = 90^\circ \\ \Rightarrow \widehat {HBC} + \widehat {BCA} = 90^\circ \end{array}\)
\( \Rightarrow \widehat {HBC} = \widehat {BAC}\) hay \(\widehat {HBC} = \widehat {BAH}\)
Xét tam giác HAB và tam giác HBC có:
\(\widehat {BAH} = \widehat {CBH}\) và \(\widehat {BHA} = \widehat {CHB} = 90^\circ \)
\( \Rightarrow \Delta HAB \backsim \Delta HBC\)
b) Vì \(\Delta HAB \backsim \Delta HBC\) nên
\(\begin{array}{l}\frac{{HA}}{{HB}} = \frac{{HB}}{{HC}}\\ \Rightarrow H{B^2} = HA.HC\\ \Rightarrow H{B^2} = 4.9 = 36\\ \Rightarrow HB = 6cm\end{array}\)
Ta chứng minh được \(\Delta HAD \backsim \Delta HDC\)
\(\begin{array}{l} \Rightarrow \frac{{HA}}{{HD}} = \frac{{HD}}{{HC}}\\ \Rightarrow H{D^2} = HA.HC\\ \Rightarrow H{D^2} = 4.9 = 36\\ \Rightarrow HD = 6cm\end{array}\)
Vậy \(HB = HD = 6cm\).

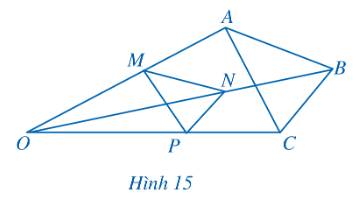
Xét tam giác OAB có \(\frac{{OM}}{{MA}} = \frac{{ON}}{{NB}}\) (Định lý Thales)
Xét tam giác OBC có \(\frac{{OP}}{{PC}} = \frac{{ON}}{{NB}}\) (Định lý Thales)
Từ đó ta có \(\frac{{OM}}{{MA}} = \frac{{OP}}{{PC}}\).
Xét tam giác OAC với \(\frac{{OM}}{{MA}} = \frac{{OP}}{{PC}} \Rightarrow MP\parallel AC\) (Hệ quả của định lý Thales).

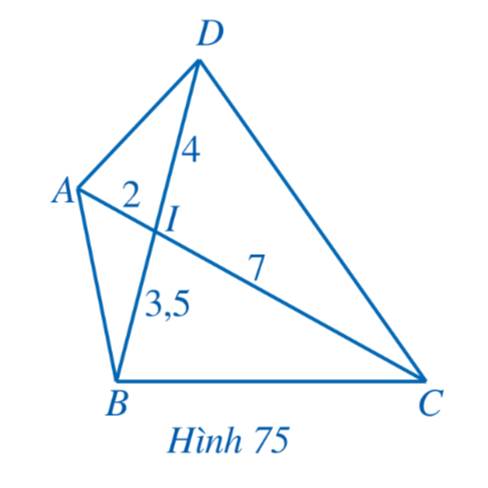
a) Ta thấy \(\frac{{IA}}{{ID}} = \frac{2}{4} = \frac{1}{2};\,\,\frac{{IB}}{{IC}} = \frac{3}{6} = \frac{1}{2}\)
\( \Rightarrow \frac{{IA}}{{ID}} = \frac{{IB}}{{IC}}\)
Mà \(\widehat {AIB} = \widehat {DIC}\) (hai góc đối đỉnh)
Xét tam giác IAB và tam giác IDC có:
\(\frac{{IA}}{{ID}} = \frac{{IB}}{{IC}}\) và \(\widehat {AIB} = \widehat {DIC}\)
\( \Rightarrow \)\(\Delta IAB \backsim \Delta IDC\) (c-g-c)
b) Ta thấy \(\frac{{IA}}{{IB}} = \frac{2}{3};\,\,\frac{{ID}}{{IC}} = \frac{4}{6} = \frac{2}{3}\)
\( \Rightarrow \frac{{IA}}{{IB}} = \frac{{ID}}{{IC}}\)
Mà \(\widehat {AID} = \widehat {BIC}\) (hai góc đối đỉnh)
Xét tam giác IAD và tam giác IBC có:
\(\frac{{IA}}{{IB}} = \frac{{ID}}{{IC}}\) và \(\widehat {AID} = \widehat {BIC}\)
\( \Rightarrow \)\(\Delta IAD \backsim \Delta IBC\) (c-g-c)





Nhìn vào biểu đồ, tương ứng với các mốc thời gian, số ở cột màu xanh biểu diễn GDP của Việt Nam và số ở cột màu đổ biểu diễn GDP của Singapore.
Ta xác định được GDP của hai nước trong các năm 2016, 2017, 2018 như sau:
Việt Nam:
Năm 2016: 205,3 tỉ đô la Mỹ
Năm 2017: 223,7 tỉ đô la Mỹ
Năm 2018: 245,2 tỉ đô la Mỹ
Singapore:
Năm 2016: 318,7 tỉ đô la Mỹ
Năm 2017: 341,9 tỉ đô la Mỹ
Năm 2018: 373,2 tỉ đô la Mỹ