Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: A(1;2); B(2;1)
=>\(\overrightarrow{AB}=\left(1;-1\right)\)
=>VTPT là (1;1)
Phương trình đường thẳng AB là:
1(x-1)+2(y-1)=0
=>x-1+2y-2=0
=>x+2y-3=0
b:
M(1;3); Δ: 3x+4y+10=0
Khoảng cách từ M đến Δ là:
\(d\left(M;\text{Δ}\right)=\dfrac{\left|1\cdot3+3\cdot4+10\right|}{\sqrt{3^2+4^2}}=\dfrac{\left|3+12+10\right|}{5}=5\)

Đáp án D
Ta gọi M(a ; 0)
Đường thẳng AB qua B(0 ; 3) và nhận A B → ( - 3 ; 4 ) làm VTCP và n → ( 4 ; 3 ) làm VTPT nên có pt :
4(x-0) + 3( y-3) =0 hay 4x + 3y -9= 0 và AB= 5
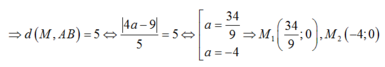

Đáp án D
Đường thẳng đi qua 2 điểm A và B có vectơ chỉ phương là ![]() suy ra tọa độ vectơ pháp tuyến là ( 4;3) .
suy ra tọa độ vectơ pháp tuyến là ( 4;3) .
Suy ra phương trình AB: 4( x-3) + 3( y+ 1) = 0 hay 4x+ 3y -9=0
Do M nằm trên Ox nên M( x; 0)
Do d(M; AB)=1 nên
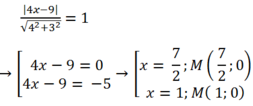

Gọi M(x,y)
Theo bài ra ta có:
d(M,AB)=\(\frac{x-3y+5}{\sqrt{10}}\) =\(\frac{\sqrt{10}}{2}\)
=>x=3y (1)
CosAMB=\(\frac{y^2-5y+6+x^2-5x+4}{\sqrt{\left(y-2\right)^2+\left(1-x\right)^2}\cdot\sqrt{\left(y-3\right)^2+\left(4-x\right)^2}}\) =\(-\frac{\sqrt{2}}{2}\) (2)
thay (1) vào (2) có lẽ ra pt bậc 4 đó giải tiếp nhé

Đường tròn (C) tâm \(I\left(1;-2\right)\) bán kính \(R=\sqrt{5}\)
Điểm M thuộc (C) thỏa mãn khoảng cách từ M tới \(\Delta\) lớn nhất khi M là giao điểm của (C) và đường thẳng d qua I và vuông góc \(\Delta\)
Phương trình d có dạng:
\(2\left(x-1\right)-1\left(y+2\right)=0\Leftrightarrow2x-y-4=0\)
Hệ pt tọa độ giao điểm (C) và d:
\(\left\{{}\begin{matrix}x^2+y^2-2x+4y=0\\y=2x-4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+\left(2x-4\right)^2-2x+4\left(2x-4\right)=0\\y=2x-4\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-2x=0\\y=2x-4\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}M\left(0;-4\right)\\M\left(2;0\right)\end{matrix}\right.\)
Với \(M\left(0;-4\right)\Rightarrow d\left(M;\Delta\right)=\dfrac{\left|-2.4+7\right|}{\sqrt{1^2+2^2}}=\dfrac{1}{\sqrt{5}}\)
Với \(M\left(2;0\right)\Rightarrow d\left(M;\Delta\right)=\dfrac{\left|2+0+7\right|}{\sqrt{1^2+2^2}}=\dfrac{9}{\sqrt{5}}\)
Do \(\dfrac{9}{\sqrt{5}}>\dfrac{1}{\sqrt{5}}\) nên \(M\left(2;0\right)\) là điểm cần tìm

Gọi e thuộc ab 2 tiếp tuyến của C qua E lần lượt là H,K biết HK=2