Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

3. Gọi tam giác đó là ABC với góc A vuông, các đường trung trực ứng với cạnh AB, AC lần lượt là MN,PQ; D là trung điểm cạnh huyền AC
Có : MN song song với AC và đi qua M là trung điểm của AB => N là trung điểm của BC(t/c đường trung bình) => N trùng với D
PQ song song với AB và đi qua P là trung điểm của AC => Q là trung điểm của BC(t/c đường trung bình) => Q trùng với D
MN cắt PQ tại trung điểm D của BC
Mà đường trung bình của BC đi qua D
=> Giao điểm 3 đường trung trực là D trung điểm cạnh huyền BC

Câu 1 : Góc lớn nhất là góc A ( đáp án đúng là a )
Câu 2 : Cạnh lớn nhất là cạnh AC ( đáp án đúng là b )
Câu 3 : Trong tam giác, điểm cách đều 3 cạnh là giao điểm của ba đường phân giác ( đáp án đúng là đáp án c )
Câu 4 : Chu vi tam giác đó là 22cm ( đáp án đúng là đáp án c )
Câu 5 : Bộ ba đoạn thẳng không thể là ba cạnh của một tam giác là 3cm,2cm,6cm ( đáp án đúng là đáp án b )
Câu 6 : Khi đó ta có MP>NP>MN ( đáp án đúng là đáp án c )
Câu 7 : Trọng tâm của tam giác là giao điểm của ba đường trung tuyến ( đáp án đúng là đáp án a )

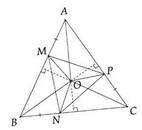
a, Vì \(\Delta ABC\) đều và \(O\) là giao điểm 3 đường trung trực nên \(AO\) là tia phân giác của \(\widehat{A}\)
\(\Rightarrow\widehat{MAO}=\dfrac{\widehat{BAC}}{2}=30^o\)
b, Tương tự a, \(\widehat{OCB}=30^o\)
Chứng minh được: \(\Delta MAO=\Delta OPC\left(c.g.c\right)\)
Ta có: \(\Delta MAO=\Delta OPC\Rightarrow OM=OP\left(1\right)\)
c, Tương tự b
\(\Delta MAO=\Delta NBO\left(c.g.c\right)\)
\(\Rightarrow ON=OM\left(2\right)\)
Từ (1) và (2) suy ra O là giao điểm
3 đương trung trực của tam giác MNP

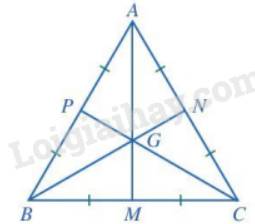
Gọi M, N, P lần lượt là các trung điểm của các đoạn thẳng BC, AC, AB.
Ta có: G là giao điểm của ba đường trung tuyến trong tam giác ABC.
Mà G cũng là giao điểm của ba đường trung trực trong tam giác ABC nên AM, BN, CP là các đường trung trực của tam giác ABC hay \(AM \bot BC;BN \bot AC;CP \bot AB\).
Xét tam giác ABM và tam giác ACM có:
AM chung;
\(\widehat {AMB} = \widehat {AMC} (= 90^\circ \))(vì \(AM \bot BC\));
BM = MC (M là trung điểm của BC).
Vậy \(\Delta ABM = \Delta ACM\)(c.g.c). Suy ra: AB = AC ( 2 cạnh tương ứng). (1)
Tương tự ta có:
\(\Delta BNA = \Delta BNC\)(c.g.c). Suy ra: AB = BC( 2 cạnh tương ứng). (2)
Từ (1) và (2) suy ra: AB = BC = AC.
Vậy tam giác ABC đều.

????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????

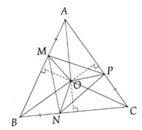
c, giao điểm 2 đường phân giác
chúc bn hok tốt!
đúng thì k cho mk nha!
mk ghi nhầm, 2 sửa thành 3 nha