Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bạn coi lại đề, 2 đường thẳng xuất phát từ B nhưng lại song song với nhau, điều này hoàn toàn vô lý
Tọa độ A là:
2x-3y+12=0 và 2x+3y=0
=>x=-3 và y=2
Tọa độ M, M là trung điểm của BC là M(x;-3x/2)
Phương trình BC sẽ là: 3x+2y+c=0
Thay x=4 và y=-1 vào BC, ta được:
3*4+2*(-1)+c=0
=>c+12-2=0
=>c=-10
=>BC: 3x+2y-10=0
=>B(x;5-1,5x); y=5-1,5x
B(x;5-1,5x); C(4;-1); M(x;-3x/2)
Theo đề, ta có: x=(4+x)/2 và -1,5x=(5x-1)/2
=>2x=x+4 và -3x=5x-1
=>x=4 và -8x=-1(loại)
=>Không có điểm B nào thỏa mãn
B A K C H(-1;1) 4x+3y-13=0 x-y+1=0
Gọi K là điểm đối xứng với H qua đường phân giác trong góc A. Khi đó K thuộc đường thẳng AC. Đường thẳng HK có phương trình \(x+y+2=0\)
Gọi I là giao điểm của HK và đường phân giác trong góc A thì I có tọa độ là nghiệm của hệ :
\(\begin{cases}x-y+2=0\\x+y+2=0\end{cases}\)\(\Leftrightarrow\begin{cases}x=-2\\y=0\end{cases}\)\(\Rightarrow I\left(-2;0\right)\)
I là trung điểm HK nên suy ta \(K\left(-3;1\right)\)
Khi đó AC :\(3\left(x+3\right)-4\left(y-1\right)=0\Leftrightarrow3x-4y+1=0\)
A có tọa độ thỏa mãn : \(\begin{cases}x-y+2=0\\3x-4y+13=0\end{cases}\)\(\Leftrightarrow\begin{cases}x=5\\y=7\end{cases}\)\(\Leftrightarrow A\left(5;7\right)\)
AB có phương trình : \(\frac{x+1}{6}=\frac{y+1}{8}\Leftrightarrow4x-3y+1=0\)
B có tọa độ thỏa mãn : \(\begin{cases}4x+3y-1=0\\4x-3y+1=0\end{cases}\)\(\Leftrightarrow\begin{cases}x=0\\y=\frac{1}{3}\end{cases}\)\(\Rightarrow B\left(0;\frac{1}{3}\right)\)
HC có phương trình : \(3\left(x+1\right)+4\left(y+1\right)=0\Leftrightarrow30+4y+7=0\)
C có tọa độ thỏa mãn hệ phương trình :
\(\begin{cases}3x+4y+7=0\\3x-4y+13=0\end{cases}\)\(\begin{cases}x=-\frac{10}{3}\\y=\frac{3}{4}\end{cases}\)\(\Rightarrow C\left(-\frac{10}{3};\frac{3}{4}\right)\)
cho mk hs: tai sao K thuoc duong thang AC thi HK co phuong trinh nhu vay ak
Tọa độ B là nghiệm: \(\left\{{}\begin{matrix}x+y+1=0\\x-2y-2=0\end{matrix}\right.\) \(\Rightarrow B\left(0;-1\right)\)
Gọi vtpt của đường thẳng CM (cũng là đường cao kẻ từ C) có tọa độ \(\left(a;b\right)\)
H là chân đường cao kẻ từ B
\(cos\widehat{HBC}=\dfrac{\left|1.1+1.\left(-2\right)\right|}{\sqrt{1^2+1^2}.\sqrt{1^2+\left(-2\right)^2}}=\dfrac{1}{\sqrt{10}}\)
\(\Rightarrow cos\widehat{MCB}=cos\widehat{HBC}=\dfrac{1}{\sqrt{10}}=\dfrac{\left|a+b\right|}{\sqrt{a^2+b^2}.\sqrt{1^2+1^2}}\)
\(\Leftrightarrow\sqrt{a^2+b^2}=\sqrt{5}\left|a+b\right|\Leftrightarrow a^2+b^2=5\left(a+b\right)^2\)
\(\Leftrightarrow2a^2+5ab+2b^2=0\Leftrightarrow\left(a+2b\right)\left(2a+b\right)=0\)
Chọn \(\left(a;b\right)=\left[{}\begin{matrix}\left(2;-1\right)\\\left(1;-2\right)\end{matrix}\right.\) (trường hợp (1;-2) loại do song song BH)
\(\Rightarrow\) Phương trình đường cao kẻ từ C:
\(2\left(x-2\right)-1\left(y-1\right)=0\Leftrightarrow2x-y-3=0\)
Tọa độ C là nghiệm: \(\left\{{}\begin{matrix}x+y+1=0\\2x-y-3=0\end{matrix}\right.\) \(\Rightarrow C\left(...\right)\)
Gọi N là trung điểm BC \(\Rightarrow\) tọa độ N
Tam giác ABC cân tại A \(\Rightarrow\) AN là trung tuyến đồng thời là đường cao
\(\Rightarrow\) Đường thẳng AN vuông góc BC \(\Rightarrow\) nhận (1;-1) là 1 vtpt và đi qua N
\(\Rightarrow\) Phương trình AN
Đường thẳng AB vuông góc CM nên nhận (1;2) là 1 vtpt
\(\Rightarrow\) Phương trình AB (đi qua B và biết vtpt)
\(\Rightarrow\) Tọa độ A là giao điểm AB và AN
Từ 3 đường thẳng cho trước , ta xác định được tọa độ của A và B:
xA-3yA+11=0, 3xA+7yA-15 =0 suy ra xA=-2, yA=3
xB-3yB=11=0; 3xB-5yB+13=0, suy ra xB=4; yB=5
a) Gọi đường thẳng qua BC là y=ax+b; vì nó vuông góc với đt AH 3x+7y-15=0, vậy a= 7/3
yB=(7/3).xB+b từ đó b= yB - 7xB/3= 5-7.4/3= -13/3
Vậy đt qua BC có pt: y= 7x/3 -13/3
b) Gọi pt đt qua AC là y=cx+d. c= -5/3 (vì nó vuông góc với đường 3x-5y+13)
d= yA-c.xA= 3+5.(-2)/3= -1/3
Vậy pt đt qua AC là y= -5x/3 -1/3
c) Điểm C là giao điểm của dt BC và AC:
yC= 7xC/3 -13/3 và yC= -5xC/3 -1/3. Từ đó tính ra xC=1; yC=-2.
gọi pt đường cao đi qua C là y=mx+n thì m= -3 (vì nó vuông góc với đt x-3y+11=0.
n=yC-mxC= (-2)-(-3).1=1
Vậy pt đường thảng đi qua đuờng cao hạ từ c là y= -3x+1
Hòa tan 24,4g Na2CO3 va K2CO3 vào nước được dung dịch A.Them vao dung dich A 33,3g CaCl2 thay tao thanh 20g ket tua va dung dich B.Tinh phan tram ve khoi luong moi muoi trong hon hop ban dau
ta có tọa độ B là nghiệm của hệ \(\hept{\begin{cases}x-2=0\\2x+3y=1\end{cases}\Leftrightarrow B\left(2;-1\right)}\)
Từ I kẻ d' qua I và song song với BC khi đó \(d':x=-7\)
Khi đó d' cắt AC tại điểm K có tọa độ là \(\hept{\begin{cases}x=-7\\2x+3y=1\end{cases}\Leftrightarrow}K\left(-7;5\right)\), gọi H là trung điểm của BC
khi đó điểm A thuộc trung trực của KI là đường thẳng AH: \(y=1\)Do đó tọa độ A là : \(A\left(-1;1\right)\)
Do đó đường cao từ C có VTPT \(IA=\left(6,4\right)\)nên đường cao từ C là : \(3x+2y-4=0\)
AB giao AH \(\Rightarrow A=\left\{{}\begin{matrix}x-3y+11=0\\3x+7y-15=0\end{matrix}\right.\)
\(\Rightarrow A\left(-2;3\right)\)
AB giao BH \(\Rightarrow B=\left\{{}\begin{matrix}x-3y+11=0\\3x-5y+13=0\end{matrix}\right.\)
\(\Rightarrow B\left(4;5\right)\)
*\(AH\perp BC\Rightarrow BC:7x-3y+a=0\)
Mà BC đi qua B \(\Rightarrow7\times4-3\times5+c=0\Rightarrow c=-13\)
BC: \(7x-3y-13=0\)
*\(BH\perp AC\Rightarrow AC:5x+3y+c=0\)
Mà AC đi qua A \(\Rightarrow5\times\left(-2\right)+3\times3+c=0\Rightarrow c=1\)
AC: \(5x+3y+1=0\)
Chọn A.
Gọi AH là đường cao của tam giác ABC ⇒ AH ⊥ BC.
B(4;5), C(-3;2)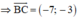
Phương trình đường cao AH đi qua A(2;-1) nhận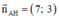
là VTPT là:
7.(x - 2) + 3.(y + 1) = 0 ⇔ 7x - 14 + 3y + 3 = 0 ⇔ 7x + 3y - 11 = 0
Vậy phương trình đường cao AH là 7x + 3y - 11 = 0.