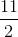Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình đường thẳng AM: \(ax+by-\dfrac{11}{2}a-\dfrac{1}{2}b=0\left(a^2+b^2\ne0\right)\)
Giả sử cạnh hình vuông có độ dài là \(a\)
\(AM^2=\dfrac{5}{4}a^2;AN^2=\dfrac{10}{9}a^2;MN^2=\dfrac{25}{36}a^2\)
Theo định lí cos: \(cosMAN=\dfrac{AM^2+AN^2-MN^2}{2.AM.AN}=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\dfrac{\left|2a-b\right|}{\sqrt{5\left(a^2+b^2\right)}}=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left(a-3b\right)\left(3a+b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=3b\\3a=-b\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}AM:3x+y-17=0\\AM:x-3y-4=0\end{matrix}\right.\)
TH1: \(AM:3x+y-17=0\Rightarrow A:\left\{{}\begin{matrix}3x+y-17=0\\2x-y-3=0\end{matrix}\right.\Rightarrow A=\left(4;5\right)\)
TH2: \(AM:x-3y-4=0\Rightarrow A:\left\{{}\begin{matrix}x-3y-4=0\\2x-y-3=0\end{matrix}\right.\Rightarrow A=\left(1;-1\right)\)

Đặt AB=a
=>\(MB=MN=a\sqrt{10};BN=2a\sqrt{5}\)
=>ΔBMN vuông cân tại M và J là trung điểm của BN
=>MJ vuông góc NJ
=>NJ: x-5=0
Tọa độ J là:
x-5=0 và 2y-7=0
=>x=5 và y=7/2
Vì J là trung điểm của BN nên B(5;1)
Gọi C(x,y), x>3
BC=2NC=2 căn 5
Ta có HPT:
(x-5)^2+(y-1)^2=20 và (x-5)^2+(y-6)^2=5
=>x=7 và y=5(nhận) hoặc x=3 và y=5(loại)
=>C(7;5)

a) Cho \(x=0\Rightarrow y=-2\)
Cho \(y=0\Rightarrow x=1\)
Nối hai điểm (0;-2) và (1;0) ta được:
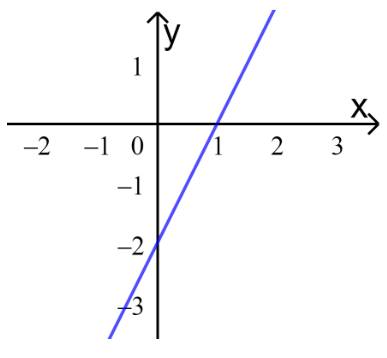
b) Thay tọa độ điểm M vào bất phương trình (3) ta được:
\(2.2 - \left( { - 1} \right) > 2 \Leftrightarrow 5 > 2\)(Luôn đúng)
Vậy (2;-1) là một nghiệm của bất phương trình (3)
c) Ta gạch đi nửa mặt phẳng không chứa M được:

Câu 1:
Do \(\Delta\) song song d nên nhận \(\left(2;-1\right)\) là 1 vtpt
Phương trình \(\Delta\) có dạng: \(2x-y+c=0\) (\(c\ne2015\))
Tọa độ giao điểm của \(\Delta\) và Ox: \(\left\{{}\begin{matrix}y=0\\2x-y+c=0\end{matrix}\right.\) \(\Rightarrow M\left(-\frac{c}{2};0\right)\)
Tọa độ giao điểm \(\Delta\) và Oy: \(\left\{{}\begin{matrix}x=0\\2x-y+c=0\end{matrix}\right.\) \(\Rightarrow N\left(0;c\right)\)
\(\overrightarrow{MN}=\left(\frac{c}{2};c\right)\Rightarrow\frac{c^2}{4}+c^2=45\Leftrightarrow c^2=36\Rightarrow\left[{}\begin{matrix}c=6\\c=-6\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}2x-y+6=0\\2x-y-6=0\end{matrix}\right.\)
Bài 2:
Bạn tham khảo ở đây:
Câu hỏi của tôn hiểu phương - Toán lớp 10 | Học trực tuyến