Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. \(\left|\frac{2x^2-x}{3x-4}\right|\ge1\) Điều kiện: \(x\ne\frac{4}{3}\)
\(\Leftrightarrow\orbr{\begin{cases}\frac{2x^2-x}{3x-4}\ge1\\\frac{2x^2-x}{3x-4}\le-1\end{cases}}\Leftrightarrow\orbr{\begin{cases}\frac{x^2-2x+2}{3x-4}\ge0\\\frac{x^2+x-2}{3x-4}\le0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x>\frac{4}{3}\\x\in(-\infty;-2]U[1;\frac{4}{3})\end{cases}}\Leftrightarrow x\in(-\infty;-2]U[1;+\infty)\backslash\left\{\frac{4}{3}\right\}\)
2.\(\hept{\begin{cases}x^2\le-2x+3\left(1\right)\\\left(m+1\right)x\ge2m-1\left(2\right)\end{cases}}\)
\(\left(1\right)\Leftrightarrow x^2+2x-3\le0\Leftrightarrow-3\le x\le1\)
+) Nếu \(m=-1\) thì (2) vô nghiệm, suy ra \(m\ne-1\)
+) Nếu \(m>-1\) thì \(\left(2\right)\Leftrightarrow x\ge\frac{2m-1}{m+1}\)
Hệ BPT có nghiệm duy nhất \(\Leftrightarrow\frac{2m-1}{m+1}=1\Leftrightarrow m=2>-1\)
+) Nếu \(m< -1\)thì \(\left(2\right)\Leftrightarrow x\le\frac{2m-1}{m+1}\)
Hệ BPT có nghiệm duy nhất \(\Leftrightarrow\frac{2m-1}{m+1}=-3\Leftrightarrow m=-\frac{2}{5}< -1\)
Vậy \(m=\left\{\frac{-2}{5};2\right\}\)
1. |2x2−x3x−4 |≥1 Điều kiện: x≠43
⇔[
| 2x2−x3x−4 ≥1 |
| 2x2−x3x−4 ≤−1 |
⇔[
| x2−2x+23x−4 ≥0 |
| x2+x−23x−4 ≤0 |
⇔[
| x>43 |
| x∈(−∞;−2]U[1;43 ) |
⇔x∈(−∞;−2]U[1;+∞)\{43 }
2.{
| x2≤−2x+3(1) |
| (m+1)x≥2m−1(2) |
(1)⇔x2+2x−3≤0⇔−3≤x≤1

a) Ta có \(\lim\limits_{x\rightarrow-\infty}\dfrac{4x+1}{-x+1}=\lim\limits_{x\rightarrow-\infty}\left(\dfrac{-4+\dfrac{1}{x}}{1+\dfrac{1}{x}}\right)=-4\)
b) Ta có \(\lim\limits_{x\rightarrow2}f\left(x\right)=\lim\limits_{x\rightarrow2}\dfrac{x^2-x-2}{x-2}=\lim\limits_{x\rightarrow2}\left(\dfrac{\left(x+1\right)\left(x-2\right)}{x-2}\right)\)
\(=\lim\limits_{x\rightarrow2}\left(x+1\right)=2+1=3\)
Để hàm số đã cho liên tục tại \(x=2\) thì \(\lim\limits_{x\rightarrow2}f\left(x\right)=f\left(2\right)=m\) hay \(m=3\).

i:
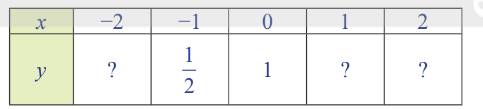
| x | -2 | -1 | 0 | 1 | 2 |
| y | 1/4 | 1/2 | 1 | 2 | 4 |
ii:
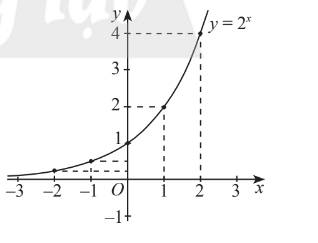
Hàm số liên tục và đồng biến trên R
\(\lim\limits_{x\rightarrow+\infty}2^x=+\infty;\lim\limits_{x\rightarrow-\infty}2^x=0\)
Tập giá trị: \((0;+\infty)\)
b:
bảng giá trị:
| x | -2 | -1 | 0 | 1 | 2 |
| y | 4 | 2 | 1 | 1/2 | 1/4 |
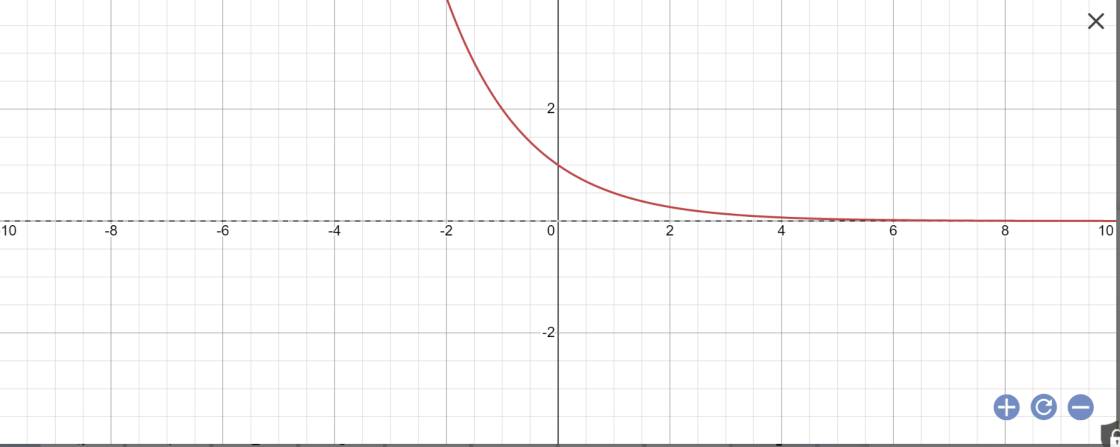
Hàm số liên tục và nghịch biến trên R
\(\lim\limits_{x\rightarrow+\infty}\left(\dfrac{1}{2}\right)^x=0;\lim\limits_{x\rightarrow-\infty}\left(\dfrac{1}{2}\right)^x=+\infty\)
Tập giá trị: (0;+\(\infty\))

Đường tròn ngoại tiếp tam giác ABC là ảnh của đường tròn (T) qua phép vị tự tâm O tỉ số \(k=2\)
\(\Rightarrow\) Phương trình đường tròn ngoại tiếp tam giác:
\(\left(x-2\right)^2+\left(y+1\right)^2=25\)
(Tọa độ tâm nhân 2 lần và bán kính nhân 2 lần)

Bài 1: dưới mẫu không biết biểu thức là gì
Bài 2:
Gọi \(M\in d\Rightarrow M\left(1+2m;3-m\right)\)
\(\Rightarrow\overrightarrow{AM}=\left(2m;5-m\right)\)
\(\Rightarrow AM^2=\overrightarrow{AM}^2=4m^2+\left(5-m\right)^2=25\)
\(\Leftrightarrow5m^2-10m+25=25\)
\(\Leftrightarrow5m\left(m-2\right)=0\Rightarrow\left[{}\begin{matrix}m=0\\m=2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}M\left(1;3\right)\\M\left(5;1\right)\end{matrix}\right.\)

I B A C M D
Đường tròn \(\left(C\right):\left(x-1\right)^2+\left(y-1\right)^2=25\) có tâm \(I\left(1;1\right)\) và bán kính \(R=5\)
\(\overrightarrow{IA}=\left(6;8\right)\Rightarrow IA=10=2R\)=> Đường tròn (C) chia đôi IA tại C
Gọi D là trung điểm IC, ta có: \(\frac{ID}{IM}=\frac{1}{2}=\frac{IM}{IA}\)=> \(\Delta\)IDM ~ \(\Delta\)IMA (c.g.c), từ đây MA=2MD
Suy ra \(P=2\left(MD+MB\right)\ge2BD\)(không đổi)
Dấu "=" xảy ra khi M thuộc đoạn BD hay M là giao điểm của đoạn BD với (C)
*) Tìm M:
Ta có: C là trung điểm IA => \(C\left(4;5\right)\), D là trung điểm IC => \(D\left(\frac{5}{2};3\right)\)
\(\overrightarrow{BD}=\left(\frac{5}{2};-5\right)\Rightarrow BD:\hept{\begin{cases}x=\frac{5}{2}t\\y=8-5t\end{cases}}\); vì M thuộc BD nên \(M\left(\frac{5}{2}t;8-5t\right)\)
\(\overrightarrow{IM}=\left(\frac{5}{2}t-1;7-5t\right)\Rightarrow IM^2=\left(\frac{5}{2}t-1\right)^2+\left(7-5t\right)^2=R^2=25\)
\(\Leftrightarrow\orbr{\begin{cases}t=2\\t=\frac{2}{5}\end{cases}}\Rightarrow\orbr{\begin{cases}M\left(5;-2\right)\\M\left(1;6\right)\end{cases}}\)
Nếu \(M\left(5;-2\right)\)thì \(\overrightarrow{MB}=\left(-5;10\right);\overrightarrow{MD}=\left(-\frac{5}{2};5\right)\Rightarrow\overrightarrow{MB}=2\overrightarrow{MD}\)=> M nằm ngoài đoạn BD (L)
Vậy \(M\left(1;6\right)\).


A B C D H I (1;-2) ( 133 37 ; 58 37 ) BD:2x+y-4=0
1. \(\overrightarrow{AH}\left(\frac{96}{37};\frac{16}{37}\right)\). AB và CD cùng vuông góc với AH => AB,CD có VTPT cùng phương với vt AH
Đường thẳng AB: đi qua A(1;-2), VTPT (6;1) => \(AB:6\left(x-1\right)+\left(y+2\right)=0\Leftrightarrow6x+y-4=0\)
Đường thẳng CD: đi qua H(133/37;-58/37), VTPT (6;1)
=> \(CD:6\left(x-\frac{133}{37}\right)+\left(y+\frac{58}{37}\right)=0\Leftrightarrow6x+y-20=0\)
2. Xét hệ \(\hept{\begin{cases}2x+y=4\\6x+y=4\end{cases}\Leftrightarrow\hept{\begin{cases}x=0\\y=4\end{cases}\Rightarrow}B\left(0;4\right)}\)
\(\hept{\begin{cases}2x+y=4\\6x+y=20\end{cases}\Leftrightarrow\hept{\begin{cases}x=4\\y=-4\end{cases}\Rightarrow}D\left(4;-4\right)}\)
BD và AC có trung điểm là \(I\left(2;0\right)\), suy ra \(C\left(3;2\right)\).
3. Ta có: \(MA^2+MC^2=2MI^2+\frac{AC^2}{2};MB^2+MD^2=2MI^2+\frac{BD^2}{2}\)
\(\Rightarrow MA^2+MB^2+MC^2+MD^2=4MI^2+\frac{AC^2+BD^2}{2}\ge\frac{AC^2+BD^2}{2}\)(không đổi)
Vậy biểu thức đạt Min khi M trùng với I(3;2).
1. →AH(9637 ;1637 ). AB và CD cùng vuông góc với AH => AB,CD có VTPT cùng phương với vt AH
Đường thẳng AB: đi qua A(1;-2), VTPT (6;1) => AB:6(x−1)+(y+2)=0⇔6x+y−4=0
Đường thẳng CD: đi qua H(133/37;-58/37), VTPT (6;1)
=> CD:6(x−13337 )+(y+5837 )=0⇔6x+y−20=0
2. Xét hệ {
⇔{
⇒B(0;4)
{
⇔{
⇒D(4;−4)
BD và AC có trung điểm là I(2;0), suy ra C(3;2).
3. Ta có: MA2+MC2=2MI2+AC22 ;MB2+MD2=2MI2+BD22
⇒MA2+MB2+MC2+MD2=4MI2+AC2+BD22 ≥AC2+BD22 (không đổi)
Vậy biểu thức đạt Min khi M trùng với I(3;2).