Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

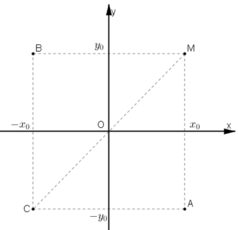
Biểu diễn các điểm trên hệ trục tọa độ ta thấy:
a) Điểm đối xứng với M(x0; y0) qua trục Ox là A(x0 ; –y0)
b) Điểm đối xứng với M(x0 ; y0) qua trục Oy là B(–x0 ; y0)
c) Điểm đối xứng với M(x0 ; y0) qua gốc O là C(–x0 ; –y0).

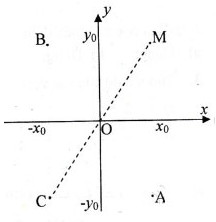
a) Hai điểm đối xứng nhau qua trục hoành thì có hoành độ bằng nhau và tung độ đối nhau.
M0 (x0; y0)=> A(x0;-y0)
b) Hai điểm đối xứng với nhau qua trục tung thì có tung độ bằng nhau còn hoành độ thì đối nhau.
M0 (x0; y0) => B(-x0;y0)
c) Hai điểm đối xứng nhau qua gốc O thì các tọa độ tương ứng đối nhau.
M0 (x0; y0) => C(-x0;-y0)

a) Hai điểm đối xứng nhau qua trục hoành thì có hoành độ bằng nhau và tung độ đối nhau.
M0 (x0; y0)=> A(x0;-y0)
b) Hai điểm đối xứng với nhau qua trục tung thì có tung độ bằng nhau còn hoành độ thì đối nhau.
M0 (x0; y0) => B(-x0;y0)
c) Hai điểm đối xứng nhau qua gốc O thì các tọa độ tương ứng đối nhau.
M0 (x0; y0) => C(-x0;-y0)

a: A(2;4); B(1;0); C(2;2)
vecto AB=(-1;-4)
vecto DC=(2-x;2-y)
Vì ABCD là hình bình hành nên vecto AB=vecto DC
=>2-x=-1 và 2-y=-4
=>x=3 và y=6
c: N đối xứng B qua C
=>x+1=4 và y+0=4
=>x=3 và y=4

a. M đối xứng A qua B \(\Rightarrow\) B là trung điểm AM
\(\Rightarrow\left\{{}\begin{matrix}x_M=2x_B-x_A=3\\y_M=2y_B-y_A=5\end{matrix}\right.\)
\(\Rightarrow M\left(3;5\right)\)
b. Do N nằm trên trục hoành nên tọa độ có dạng: \(N\left(x;0\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AN}=\left(x-1;-3\right)\\\overrightarrow{BN}=\left(x-2;-4\right)\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}AN=\sqrt{\left(x-1\right)^2+9}\\BN=\sqrt{\left(x-2\right)^2+16}\end{matrix}\right.\)
\(AN=BN\Rightarrow\left(x-1\right)^2+9=\left(x-2\right)^2+16\)
\(\Rightarrow x=5\Rightarrow N\left(5;0\right)\)

a) Hai điểm đối xứng nhau qua trục Ox sẽ có cùng hoành độ và tung độ là hai số đối nhau.
\(M\left(4;3\right)\)\(\Rightarrow A\left(4;-3\right)\).
M A O 4 3 -3
b) Hai điểm đối xứng qua trục Oy sẽ có cùng tung độ và hoành độ là hai số đối nhau.
\(M\left(4;3\right)\)\(\Rightarrow A\left(-4;3\right)\).
O x y 4 -4 3 M A

D đối xứng A qua B \(\Rightarrow B\) là trung điểm AD
\(\Rightarrow\left\{{}\begin{matrix}x_B=\frac{x_A+x_D}{2}\\y_B=\frac{y_A+y_D}{2}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_D=2x_B-x_A=2.1-\left(-1\right)=3\\y_D=2y_B-y_A=2.\left(-3\right)-2=-8\end{matrix}\right.\)
\(\Rightarrow D\left(3;-8\right)\)
\(\left\{{}\begin{matrix}x_{B'}-5=2\\y_{B'}+6=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_{B'}=7\\y_{B'}=-2\end{matrix}\right.\)