Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi M là vị trí phát ra âm thanh cầu cứu trong rừng.
Gọi \({t_1},{t_2}\)lần lượt là thời gian trạm A, B nhận được tín hiệu cầu cứu (đơn vị: giây)
\( \Rightarrow {t_A} = {t_B} - 6 \Leftrightarrow {t_B} - {t_A} = 6\)
Đổi \(v = 1{\rm{ }}236{\rm{ }}km/h{\rm{ }} = \frac{{\;1236}}{{3600}}km/s = \frac{{103}}{{300}}km/s.\;\)
Ta có: \(MA = {t_A}.v;MB = {t_B}.v\)
\( \Rightarrow MB - MA = ({t_B} - {t_A}).v = 6.\frac{{103}}{{300}} = 2,06(km)\)
Như vậy, tập hợp các điểm M là một hypepol nhận A, B làm hai tiêu điểm.
Ta có: \(AB = 16 = 2c \Rightarrow c = 8\); \(\left| {MA - MB} \right| = 2,06 = 2a \Rightarrow a = 1,03\)
\( \Rightarrow {b^2} = {c^2} - {a^2} = {8^2} - 1,{03^2} = 62,9391\)
Vậy phương trình chính tắc của hypebol đó là: (H) \(\frac{{{x^2}}}{{1,0609}} - \frac{{{y^2}}}{{62,9391}} = 1\)
Do MA < MB nên M thuộc của nhánh (H) gần A.
Vậy phạm vi tìm kiếm vị trí phát ra âm thanh đó là nhánh gần A của hypebol (H) có phương trình \(\frac{{{x^2}}}{{1,0609}} - \frac{{{y^2}}}{{62,9391}} = 1\).

Gọi M là vị trí tàu thu tín hiệu. Gọi \({t_A},{t_B}\) lần lượt là thời gian tín hiệu truyền từ trạm phát A,B đến M. Theo đề bài, ta có \({t_A} - {t_B} = - 0,0005s\).
Suy ra \(MA - MB = v.{t_A} - v.{t_B} = 292000.\left( { - 0,0005} \right) = - 146km\).
Gọi (H) là hyperbol ở dạng chính tắc nhận A,B làm hai tiêu điểm và đi qua M. Khi đó ta có:
\(\left\{ \begin{array}{l}2a = \left| {MA - MB} \right| = 146\\2c = AB = 300\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 73\\c = 150\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 73\\{b^2} = {c^2} - {a^2} = 17171\end{array} \right.\)
Vậy phương trình chính tắc của (H) là: \(\frac{{{x^2}}}{{5329}} - \frac{{{y^2}}}{{17171}} = 1\).

a) Khoảng cách từ nơi phát ra tín hiệu âm thanh tới\({F_1},{F_2}\) là: \(M{F_1}, M{F_2}\) với M là điểm đặt thiết bị âm thanh.
Rõ ràng \(M{F_1} > M{F_2}\) do thiết bị tại \({F_2}\) nhận được tín hiệu sớm hơn.
b) Có liên quan.
Gọi t là thời gian thiết bị tại \({F_2}\) nhận được tín hiệu.
Ta có: \(M{F_2}=t.343\)
Tại \({F_1}\), thời gian thiết bị nhận được tín hiệu là: \(t+2\)
=> \(M{F_1}=(t+2).343\)
=> \(M{F_1} - M{F_2} =(t+2).343 - t.343=2.343=686\)
Vậy tập hợp các điểm M mà tại đó phát ra tín hiệu âm thanh để thiết bị tại \({F_2}\) nhận được sớm hơn 2 giây thỏa mãn \(M{F_1} - M{F_2} =686\)

a) Vị trí ban đầu ứng với \(t = 0\), suy ra vật thể ở vị trí có tọa độ là \(A\left( {2;5} \right)\).
Vị trí kết thúc ứng với \(t = 180\) , suy ra vật thể ở vị trí có tọa độ là \(B\left( {2;3} \right)\).
b) Từ đẳng thức \({\left( {\sin {t^o}} \right)^2} + {\left( {\cos {t^o}} \right)^2} = 1\) ta suy ra \({\left( {{x_M} - 2} \right)^2} + {\left( {{y_M} - 4} \right)^2} = 1\)
Do đó, M thuộc đường tròn \(\left( C \right)\) có phương trình \({\left( {x - 2} \right)^2} + {\left( {y - 4} \right)^2} = 1\)
Đường tròn có tâm \(I\left( {2;4} \right)\), bán kính \(R = 1\) và nhận AB làm đường kính.
Khi \(t \in \left[ {0;180} \right]\) thì \(\sin t \in \left[ {0;1} \right]\) và \(\cos t \in \left[ { - 1;1} \right]\). Do đó, \(2 + \sin {t^o} \in \left[ {2;3} \right]\) và \(4 + \cos {t^o} \in \left[ {3;5} \right]\).
Vậy quỹ đạo của vật thể là nửa đường tròn đường kính AB vẽ trên nửa mặt phẳng chứa điểm \(C\left( {3;0} \right)\) bờ AB.

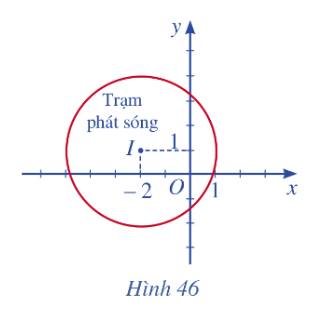
a) Phương trình đường tròn mô tả ranh giới bên ngoài của vùng phủ sóng là: \({\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} = 9\)
b) Khoảng cách từ tâm I đến A là: \(IA = \sqrt {{{\left( { - 1 + 2} \right)}^2} + {{\left( {3 - 1} \right)}^2}} = \sqrt 5 \)
Do \(IA < 3\) nên điểm A nằm trong đường tròn ranh giới. Vậy nên người A có thể dịch vụ của trạm.
c) Khoảng cách từ tâm I đến B là: \(IB = \sqrt {{{\left( { - 3 + 2} \right)}^2} + {{\left( {4 - 1} \right)}^2}} = \sqrt {10} \)
Khoảng cách ngắn nhất theo đường chim bay để 1 người ở B di chuyển đến vùng phủ sóng là:
\(IB - R = \sqrt {10} - 3\left( {km} \right)\)

Bình phương hai vế ta được:
\(\begin{array}{l}{(8 - 40x)^2} + {(7 - 40x)^2} = 25\\ \Leftrightarrow 64 - 640x + 1600{x^2} + 49 - 560x + 1600{x^2} = 25\\ \Leftrightarrow 3200{x^2} - 1200x + 88 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = \frac{{11}}{{40}}\\x = \frac{1}{{10}}\end{array} \right.\end{array}\)
Vậy phương trình có hai nghiệm là \(x = \frac{{11}}{{40}}\) và \(x = \frac{1}{{10}}\).


Gọi M (x; y) là vị trí của tâm bão tại thời điểm t giờ.
Tâm bão chuyển động đều từ A (13,8; 108,3) đến B (14,1;106,3).
Khi đó ta có: \(\overrightarrow {AM} = \frac{t}{{12}}.\overrightarrow {AB} \)
\(\begin{array}{l} \Leftrightarrow (x - 13,8;y - 108,3) = \frac{t}{{12}}.(14,1 - 13,8;106,3 - 108,3)\\ \Leftrightarrow (x - 13,8;y - 108,3) = \frac{t}{{12}}.(0,3; - 2)\\ \Leftrightarrow \left\{ \begin{array}{l}x - 13,8 = \frac{t}{{40}}\\y - 108,3 = - \frac{t}{6}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 13,8 + \frac{t}{{40}}\\y = 108,3 - \frac{t}{6}\end{array} \right.\end{array}\)
Vậy tại thời điểm t giờ, tâm bão ở vị trí \(M\left( {13,8 - \frac{t}{{40}};108,3 - \frac{t}{6}} \right)\)

Gọi B(x; y) là vị trí của tàu (trên mặt phẳng tọa độ) tại thời điểm sau khi khởi hành 1,5 giờ.
Do tàu khởi hành từ A đi chuyển với vận tốc được biểu thị bởi vectơ \(\overrightarrow v = \left( {3;4} \right)\) nên cứ sau mỗi giờ, tàu đi chuyển được một quãng bằng \(\left| {\overrightarrow v } \right|\).
Vậy sau 1,5 giờ tàu di chuyển tới B, ta được: \(\overrightarrow {AB} = 1,5.\overrightarrow v \)
\(\begin{array}{l} \Leftrightarrow (x - 1;y - 2) = 1,5\;.\left( {3;4} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}x - 1 = 4,5\\y - 2 = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5,5\\y = 8\end{array} \right.\end{array}\)
Vậy sau 1,5 tàu ở vị trí (trên mặt phẳng tọa độ) là B(5,5; 8).
Gọi J là vị trí âm thanh phát đi. Ta có J cách đều O, A, B. Do đó J là giao của hài đường trun trực \({d_1},{d_2}\) tương ứng của OA, OB. Đường thẳng \({d_1}\) đi qua trung điểm M của OA và vuông góc với OA. Ta có \(M\left( {\frac{1}{2};0} \right)\) và \(\overrightarrow {{n_{{d_1}}}} = \overrightarrow {OA} = \left( {1;0} \right)\).
Phương trình đường thẳng \({d_1}\) là \(1\left( {x - \frac{1}{2}} \right) + 0\left( {y - 0} \right) = 0 \Leftrightarrow x = \frac{1}{2}\).
Tương tự, phương trình đường thẳng \({d_2}\) là \(x + 3y - 5 = 0\).
Tọa độ điểm J là nghiệm của hệ \(\left\{ \begin{array}{l}x = \frac{1}{2}\\x + 3y - 5 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{1}{2}\\y = \frac{3}{2}\end{array} \right.\).
Vậy \(J\left( {\frac{1}{2};\frac{3}{2}} \right)\).