Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Áp dụng công thức tọa độ trung điểm:
\(\left\{{}\begin{matrix}x_I=\frac{x_A+x_B}{2}=2\\y_I=\frac{y_A+y_B}{2}=1\end{matrix}\right.\)
\(\Rightarrow I\left(2;1\right)\)
tham khảo
Gọi M' là điểm đối xứng của M qua AC. Ta có M' thuộc đường thẳng BC.
Phương trình đường thẳng MM' là 1(x - 6) - 1(y - 2) = 0 <=> x - y - 4 = 0. Gọi H = AC ∩ MM'
Tọa độ của H thỏa mãn hệ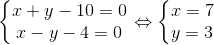 
=> H(7; 3)
H là trung điểm của MM'. Suy ra M'(8; 4)
Gọi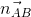 
= (a; b) . Vì hai đường thẳng AB và AC tạo với nhau một góc 450 nên ta có:
cos 450 =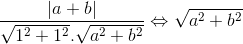 
= |a + b| ⇔ ab = 0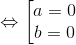
TH1: a = 0, phương trình đường thẳng AB, BC lần lượt là y = 8, x = 8. Suy ra: B(8; 8)
TH2: b = 0, phương trình đường thẳng AB, BC lần lượt là y = 5, x = 4. Suy ra: B(5; 4)
Gọi M là trung điểm AB
\(\Rightarrow\left\{{}\begin{matrix}x_M=\frac{x_A+x_B}{2}=\frac{1+0}{2}=\frac{1}{2}\\y_M=\frac{y_A+y_B}{2}=\frac{0-2}{2}=-1\end{matrix}\right.\)
\(\Rightarrow M\left(\frac{1}{2};-1\right)\)
Gọi I là TĐ AB
\(\Rightarrow\left\{{}\begin{matrix}x_I=\frac{x_A+x_B}{2}\\y_I=\frac{y_A+y_B}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_I=\frac{1+0}{2}\\y_I=\frac{0-2}{2}\end{matrix}\right.\Rightarrow I\left(\frac{1}{2};-1\right)\)
\(\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_B}{2}=\dfrac{-1+3}{2}=1\\y_I=\dfrac{y_A+y_B}{2}=\dfrac{5+\left(-1\right)}{2}=2\end{matrix}\right.\)
\(\Rightarrow I\left(1;2\right)\)
Giúp mik với