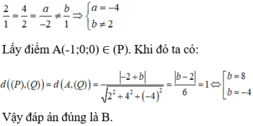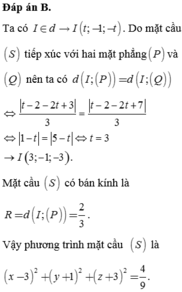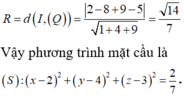Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
Phương trình (S): x2 + y2 + z2 + 4x - 6y + m = 0 là phương trình mặt cầu <=> m < 13
Khi đó (S) có tọa độ tâm I (-2;3;0) bán kính ![]()
Gọi M (x;y;z) là điểm bất kỳ thuộc Δ.
Tọa độ M thỏa mãn hệ: 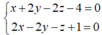
Đặt y = t ta có: 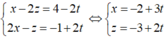
=> Δ có phương trình tham số: 
Δ đi qua điểm N (-2; 0; -3) và có vectơ chỉ phương ![]()
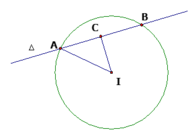
Giả sử mặt cầu (S) cắt Δ tại hai điểm phân biệt A, B sao cho AB = 8. Gọi (C) là đường tròn lớn chứa đường thẳng Δ. Khi đó IC2 = R2 - AC2 = 13 - m - 42 = -m - 3
N (0;-3;-3)

Vậy mặt cầu (S) cắt Δ tại hai điểm phân biệt A, B sao cho AB = 8
<=> -m - 3 = 9 <=> m = -12

Chọn C.
Trên mặt phẳng (Q): x + 2y - 2z + 1 = 0 chọn điểm M (-1;0;0).
Do (P) song song với mặt phẳng (Q) nên phương trình của mặt phẳng (P) có dạng: x + 2y - 2z + D = 0 với D ≠ 1.

Vậy có hai mặt phẳng thỏa mãn: x + 2y – 2z + 10 = 0 và x + 2y -2z – 8 = 0.

Chọn D.
Mặt cầu (S) có tâm I(-1;2;1) và bán kính
![]()
Do (P) song song với mặt phẳng (Q) nên phương trình của mặt phẳng (P) có dạng:
x + 2y – 2z + D = 0 với D ≠ 1.
Vì (P) tiếp xúc với mặt cầu (S) nên d(I;(P)) = R = 3
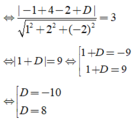
Vậy có hai mặt phẳng thỏa mãn: x + 2y – 2z – 10 = 0 và x + 2y – 2z + 8 = 0

a. Mặt phẳng (P) có (3;-2;2) là 1 vtpt nên d nhận (3;-2;2) là 1 vtcp
Phương trình tham số d: \(\left\{{}\begin{matrix}x=1+3t\\y=2-2t\\z=-1+2t\end{matrix}\right.\)
b. \(\overrightarrow{n_{\left(P\right)}}=\left(1;1;1\right)\) ; \(\overrightarrow{n_{\left(P'\right)}}=\left(1;-1;1\right)\)
\(\left[\overrightarrow{n_{\left(P\right)}};\overrightarrow{n_{\left(P'\right)}}\right]=\left(2;0;-2\right)=2\left(1;0;-1\right)\)
\(\Rightarrow\) d nhận (1;0;-1) là 1 vtcp nên pt có dạng: \(\left\{{}\begin{matrix}x=1+t\\y=-2\\z=3-t\end{matrix}\right.\)
c. \(\overrightarrow{u_{\Delta}}=\left(3;2;1\right)\) ; \(\overrightarrow{u_{\Delta'}}=\left(1;3;-2\right)\)
\(\left[\overrightarrow{u_{\Delta}};\overrightarrow{u_{\Delta'}}\right]=\left(-7;7;7\right)=7\left(-1;1;1\right)\)
Đường thẳng d nhận (-1;1;1) là 1 vtcp nên pt có dạng: \(\left\{{}\begin{matrix}x=-1-t\\y=1+t\\z=3+t\end{matrix}\right.\)

Lần sau em đăng bài ở học 24 để mọi người giúp đỡ em nhé!
Link đây: Cộng đồng học tập online | Học trực tuyến
1. Gọi I là tâm của mặt cầu cần tìm
Vì I thuộc d
=> I( a; -1; -a)
Mặt cầu tiếp xúc với hai mặt phẳng (p), (Q). nên ta co:
d(I; (P))=d(I;(Q))
<=> \(\frac{\left|a+2\left(-1\right)+2\left(-a\right)+3\right|}{\sqrt{1^2+2^2+2^2}}=\frac{\left|a+2\left(-1\right)+2\left(-a\right)+7\right|}{\sqrt{1^2+2^2+2^2}}\)
\(\Leftrightarrow\frac{\left|-a+1\right|}{3}=\frac{\left|-a+5\right|}{3}\Leftrightarrow a=3\)
=> I(3; -1; -3) ; bán kinh : R=d(I; P)=2/3
=> Phương trình mặt cầu:
\(\left(x-3\right)^2+\left(y+1\right)^2+\left(z+3\right)^2=\frac{4}{9}\)
đáp án C.
2. Gọi I là tâm mặt cầu: I(1; -1; 0)
Ta có: Phương trình mặt phẳng (P) tiếp xúc vs mặt Cầu S tại M
=> IM vuông góc vs mặt phẳng (P)
=> \(\overrightarrow{n_p}=\overrightarrow{MI}=\left(1;0;0\right)\)
=> Phương trình mặt phẳng (P) có véc tơ pháp tuyến: \(\overrightarrow{n_p}\)và qua điểm M
1(x-0)+0(y+1)+0(z-0) =0<=> x=0
đáp án B
3.
\(f\left(x\right)=\dfrac{1}{256}\left(2x+3\right)^{10}=\dfrac{1}{256} \sum \limits_{k=0} ^{10}C_{k}^{10}(2x)^k.3^{10-k}\)
Để có hệ số x^8 thì k=8 khi đó hệ số của x^8 là:
\(\dfrac{1}{256}C_{8}^{10}.2^8.3^{10-8}=405\)
đáp án D
4.
pt <=> \(\left(2.5\right)^{x^2-3}=10^{-2}.10^{3x-3}\)
\(\Leftrightarrow10^{x^2-3}=10^{3x-5}\)
\(\Leftrightarrow x^2-3=3x-5\Leftrightarrow x^2-3x+5=0\)
=> theo định lí viet tổng các nghiệm bằng 3, tích các nghiệm bằng 5
Đáp án A

a) Hai mặt phẳng cắt nhau, vì 1: 2: (-1) ≠ 2: 3: (-7)
b) Hai mặt phẳng cắt nhau, vì: 1: (-2): 1 ≠ 2: (-1): 4
c) Hai mặt phẳng song song, vì: 1/2=1/2=1/2 ≠ -1/3
d) Hai mạt phẳng cắt nhau, vì: 3: (-2): 3 ≠ 9: (-6): (-9)
e) Hai mặt phẳng trung nhau, vì: 1/10=-1/(-10)=2/20=-4/(-40).
#rin

Đáp án C
Phương pháp
Gọi H là hình chiếu của B trên mặt phẳng (Q) đi qua A và song song với (P). Khi đó
![]()
![]()
Cách giải
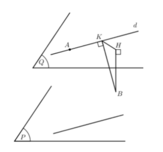
![]()
Gọi (Q) là mặt phẳng đi qua A và song song với (P) ta tìm được phương trình mặt phẳng (Q): (P): x-2y+2z-5=0, khi đó d ∈ (Q)
Gọi H là hình chiếu của B trên (Q) ta có
![]()
![]()
Phương trình đường thẳng d’ đi qua B và vuông góc với (Q) là
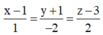
![]()
![]()
![]()
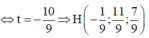
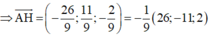
Vậy phương trình đường thẳng d cần tìm là d:
x + 3 26 = y 11 = z - 1 2

Đáp án B
Muốn khoảng cách giữa hai mặt phẳng (P) và (Q) lớn hơn 0 thì trước hết hai mặt phẳng đó phải song song (nếu hai mặt phẳng đó trùng nhau hoặc cắt nhau thì khoảng cách giữa chúng sẽ bằng 0). Do đó ta có: