Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta biết rằng có duy nhất một đường thẳng đi qua một điểm cho trước, vuông góc với một đường thẳng cho trước và có vô số đường thẳng đi qua một điểm cho trước cắt một đường cho trước. Bởi vì, có duy nhất một đường vuông góc kẻ từ điểm A đến đường thẳng d và có vô số đường xiên kẻ từ điểm A đến đường thẳng d.
(A) Đúng
(B) Sai
(C) Sai
(D) Đúng
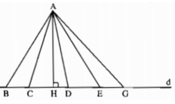
Trong hình AH là đường vuông góc duy nhất và AB, AC, AD, AE, AG là những đường xiên kẻ từ A đến d (có thể kẻ được vô số đường xiên như thế)

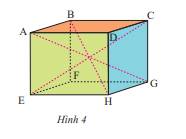
- Các góc ở đỉnh F là: góc BFE, góc BFG, góc EFG
- Các đường chéo được vẽ trong hình là: BH, AG, CE.
- Đường chéo chưa được vẽ là: DF

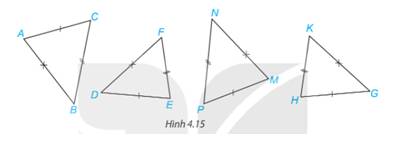
Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)

Xét \(\Delta ABC\) và \(\Delta MNP\) có:
\(\begin{array}{l}AB = MN\\BC = NP\\AC = MP\end{array}\)
Vậy\(\Delta ABC\) =\(\Delta MNP\)(c.c.c)
Xét \(\Delta DEF\) và \(\Delta GHK\) có:
\(\begin{array}{l}DE = GH\\EF = HK\\DF = GK\end{array}\)
Vậy\(\Delta DEF\)=\(\Delta GHK\) (c.c.c)

Đoạn thẳng đơn vị được chia thành 6 phần bằng nhau, lấy một đoạn làm đơn vị mới, đơn vị mới bằng \(\frac{1}{6}\) đơn vị cũ.
Điểm A nằm bên phải gốc O và cách O một đoạn bằng 10 đơn vị mới. Do đó điểm A biểu diễn số hữu tỉ \(\frac{{10}}{6} = \frac{5}{3}\)
Điểm B nằm bên trái gốc O và cách O một đoạn bằng 5 đơn vị mới. Do đó điểm B biểu diễn số hữu tỉ \(\frac{{ - 5}}{6}\)
Điểm C nằm bên trái gốc O và cách O một đoạn bằng 13 đơn vị mới. Do đó điểm C biểu diễn số hữu tỉ \(\frac{{ - 13}}{6}\)

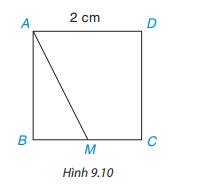
a) Đường vuông góc kẻ từ A đến BC là: AB
Đường xiên kẻ từ A đến BC là: AM
b) AB < AM (Trong các đường xiên và đường vuông góc kẻ từ 1 điểm nằm ngoài 1 đường thẳng đến đường thẳng đó thì đường vuông góc là đường ngắn nhất.)
c) Vì CB \( \bot \) AB nên khoảng cách từ C đến AB là độ dài CB = 2 cm
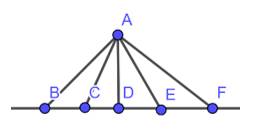


Theo hình 8 ta thấy AD là đường ngắn nhất vì AD vuông góc với BF
Các đường xiên là AB, AC, AE, AF.