Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

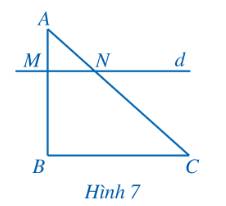
a) Quan sát hình ta thấy \(d\parallel BC\).
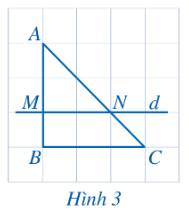
b) Ta thấy:
Độ dài AM là 2 lần cạnh của một ô vuông.
Độ dài MB là cạnh của một ô vuông.
\( \Rightarrow \frac{{AM}}{{MB}} = \frac{2}{1} = 2\)
Độ dài AN là 2 lần đường chéo của một ô vuông.
Độ dài NC là độ dài đường chéo của một ô vuông.
\( \Rightarrow \frac{{AN}}{{NC}} = \frac{2}{1} = 2\)
Vậy \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\).

Xét tam giác ABC với \(MN\parallel BC\), ta có \(\frac{{MB}}{{AB}} = \frac{{NC}}{{AC}}\) (định lý Thales).

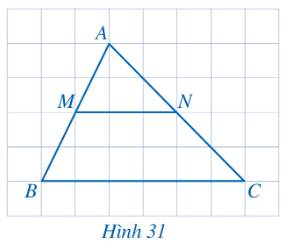
a) Vì MN là đường trung bình của tam giác ABC nên M là trung điểm AB và N là trung điểm AC.
Khi đó \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\) suy ra \(MN\parallel BC\) (Định lý Thales đảo trong tam giác ABC).
b) M là trung điểm AB nên \(\frac{{AM}}{{AB}} = \frac{1}{2}\).
Xét tam giác ABC với \(MN\parallel BC\) ta có:
\(\frac{{MN}}{{BC}} = \frac{{AM}}{{AB}} = \frac{1}{2}\) (Hệ quả của định lý Thales)

\(\begin{array}{l}\frac{{A'B'}}{{AB}} = \frac{2}{4} = \frac{1}{2}\\\frac{{A'C'}}{{AC}} = \frac{3}{6} = \frac{1}{2}\\\frac{{B'C'}}{{BC}} = \frac{4}{8} = \frac{1}{2}\end{array}\)
Ta thấy \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\)

Cho tam giác ABC vg tại AAco đg ttrung tuyến AM.Gọi D là trung điểm củ AB E là đ dối xứng vs M qua D.
a)c/m AEBM là hinhhình thoi
b)gọi I là ttung đ của AM.c/m EIC thẳng hàng
c)tam giác ABC ccó themthêm điều kiện gì thì AEBM là hình
Cụ thể như sau:
Vẽ ��,��MH,NK vuông góc ��BC thì thấy ngay �(���)=�(���)S(BMC)=S(BNC) (�S là diện tích hình)
Suy ra �(���)=�(���)S(AMC)=S(ANB) hay �(���)�(���)=�(���)�(���)S(ABC)S(AMC)=S(ACB)S(ANB), nghĩa là có câu a.
Mà có câu a thì có câu b

Ta có: AB=AM+MB=8+11=19
Vì MN//BC (gt)
=>\(\frac{AM}{AB}=\frac{AN}{AC}\Rightarrow AN=\frac{AM.AC}{AB}=\frac{11.24}{19}=\frac{264}{19}\left(cm\right)\)
=>NC=24-AN bạn tự tính

A B C M N H K
Cụ thể như sau:
Vẽ \(MH,NK\) vuông góc \(BC\) thì thấy ngay \(S\left(BMC\right)=S\left(BNC\right)\) (\(S\) là diện tích hình)
Suy ra \(S\left(AMC\right)=S\left(ANB\right)\) hay \(\frac{S\left(AMC\right)}{S\left(ABC\right)}=\frac{S\left(ANB\right)}{S\left(ACB\right)}\), nghĩa là có câu a.
Mà có câu a thì có câu b
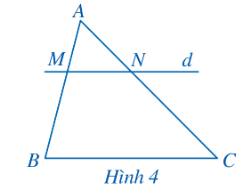

a) \(\frac{{AM}}{{MB}} = \frac{1}{2}\)
\(\frac{{AN}}{{AC}} = \frac{{1,5}}{3} = \frac{1}{2}\)
Vậy \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\).
b) Qua B kẻ đường thẳng song song với đường thẳng d, cắt AC tại C’.
Xét ∆ABC’ với MN // BC’, ta có:
\( \frac{AM}{MB}=\frac{AN}{NC′}\) (định lí Thalès).
Mà theo câu a, \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\) nên ta có \(\frac{{AN}}{{NC}} = \frac{AN}{NC′}\)
Suy ra NC = NC’ hay C và C’ là hai điểm trùng nhau.
Do đó C nằm trên đường thẳng đi qua B và song song với đường thẳng d.
Vậy đường thẳng d (đi qua M, N) song song với BC.