Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi A: “Học sinh thích môn Bóng đá”
B: “Học sinh thích môn Bóng bàn”
Do đó ta có \(P\left( A \right) = \frac{{19}}{{30}},P\left( B \right) = \frac{{17}}{{30}},P\left( {AB} \right) = \frac{{15}}{{30}}\)
Theo công thức cộng xác suất
\(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right) = \frac{{19}}{{30}} + \frac{{17}}{{30}} - \frac{{15}}{{30}} = \frac{{21}}{{30}} = \frac{7}{{10}}\)
Vậy xác suất để chọn được học sinh thích ít nhất một trong hai môn Bóng đá hoặc Bóng bàn là \(\frac{7}{{10}}\)

Không gian mẫu là số cách chọn ngẫu nhiên 3 học sinh từ 13 học sinh.
Suy ra số phần tử của không gian mẫu là ![]() .
.
Gọi A là biến cố 3 học sinh được chọn có cả nam và nữ đồng thời có cả khối 11 và khối 12
Ta có các trường hợp thuận lợi cho biến cố A là:
● Trường hợp 1. Chọn 1 học sinh khối 11; 1 học sinh nam khối 12 và 1 học sinh nữ khối 12 nên có ![]() cách.
cách.
● Trường hợp 2. Chọn 1 học sinh khối 11; 2 học sinh nữ khối 12 có ![]() cách.
cách.
● Trường hợp 3. Chọn 2 học sinh khối 11; 1 học sinh nữ khối 12 có ![]() cách.
cách.
Suy ra số phần tử của biến cố A là ![]()
Vậy xác suất cần tính 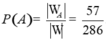
Chọn D.

Chọn A
Lời giải. Gọi số học sinh nữ trong nhóm A là x ( x ∈ ℕ * )
Gọi số học sinh nam trong nhóm B là y ( y ∈ ℕ * )
Suy ra số học sinh nữ trong nhóm B là
25 - 9 - x - y = 16 - x - y
Khi đó, nhóm A có: 9 nam, x nữ và nhóm B có
y nam, 16 - x - y nữ
Xác suất để chọn được hai học sinh nam là
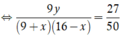
![]()
![]()
![]()
Mặt khác x + y < 16
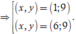
Vậy xác suất để chọn đươc hai học sinh nữ là
C 1 1 . C 6 1 C 10 1 . C 15 1 = 0 , 04

Đáp án B
Gọi số học sinh nữ trong nhóm A là x ( x ∈ ℕ * )
Gọi số học sinh nam trong nhóm B là y ( y ∈ ℕ * ) .
=> Số học sinh nữ trong nhóm B là 25 – 9 – x = 16 – x – y => x + y < 16
Khi đó, Nhóm A: 9 nam, x nữ và nhóm B: y nam, 16 – x – y nữ.
Xác suất để chọn được hai học sinh nam là
C 9 1 . C y 1 C 9 + x 1 . C 25 - 9 - x 1 = 0 , 54
⇔ 9 y ( 9 + x ) ( 16 - x ) = 27 50 .
⇒ y = 30 50 ( 9 + x ) ( 16 - x ) ⇒ x < 16 .
Vì y ∈ ℕ * ⇒ 3 50 ( 9 + x ) ( 16 - x ) ∈ N * .
=> (x, y) = {(1; 9), (6; 9), (11; 6)}.
Mặt khác x + y < 16
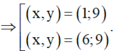
( Khi chia nhóm thì A,B có vai trò như nhau nên có 2 cặp thỏa mãn )
Vậy xác suất để chọn đươc hai học sinh nữ là 0,04.

Trong mỗi khối, XS hs trượt Toán là 0,25; trượt Lý là 0,15; trượt cả 2 môn là 0,1; trượt đúng 1 môn là 0,2; chỉ trượt Toán là 0,15; chỉ trượt Lý là 0,05; trượt ít nhất 1 môn là 0,3; ko trượt môn nào là 0,7
a) P = 0,25^2 = 0,0625
b) Câu này đề chưa rõ ràng, có nhiều cách hiểu
..1) 2 hs đó đều bị trượt ít nhất 1 môn
..2) 2 hs đó cùng bị trượt trong 1 môn nào đó (còn môn kia không trượt)
..3) 2 hs đó cùng bị trượt trong 1 môn nào đó (còn môn kia có thể trượt hoặc không)
..Nếu hiểu theo cách 1 thì P = 0,3^2 = 0,09
..Nếu hiểu theo cách 2 thì P = 0,15^2 + 0,05^2 = 0,025
..Nếu hiểu theo cách 3 thì P = 0,25^2 + 0,15^2 - 0,1^2 = 0,075
c) P = 0,7^2 = 0,49
d) Trường hợp này là biến cố đối lập với biến cố c
..P = 1 - 0,7^2 = 0,51

Kí hiệu A 1 , A 2 , A 3 lần lượt là các biến cố: Học sinh được chọn từ khối I trượt Toán, Lí, Hoá: B 1 , B 2 , B 3 lần lượt là các biến cố : Học sinh được chọn từ khối II trượt Toán, Lí, Hoá. Rõ ràng với mọi (i,j), các biến cố A i và B i độc lập.
a) 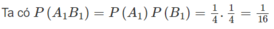
b) Xác suất cần tính là
P ( ( A 1 ∪ A 2 ∪ A 2 ) ∩ ( B 1 ∪ B 2 ∪ B 3 ) ) = P ( A 1 ∪ A 2 ∪ A 2 ) . P ( B 1 ∪ B 2 ∪ B 3 ) = 1 / 2 . 1 / 2 = 1 / 4
c) Đặt A = A 1 ∪ A 2 ∪ A 3 , B = B 1 ∪ B 2 ∪ B 3
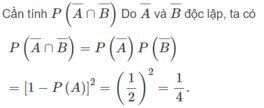
d) Cần tính P(A ∪ B)
Ta có
P(A ∪ B) = P(A) + P(B) − P(AB)
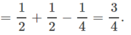

Cặp biến cố E và F không xung khắc vì nếu học sinh được chọn thích môn Bóng đá thì cả E và F có thể xảy ra vì có 2 bạn thích cả hai môn Bóng đá và Cầu lông.
Vì có 2 bạn cùng thích bóng đá và cầu lông
nên hai biến cố E và F không xung khắc

Đáp án D
Gọi A là biến cố “Học sinh được chọn đạt điểm tổng kết loại giỏi môn Hóa học”.
B là biến cố “Học sinh được chọn đạt điểm tổng kết loại giỏi môn Vật lí”.
⇒ A C = a 3 A ∪ B là biến cố “Học sinh được chọn đạt điểm tổng kết môn Hóa học hoặc Vật lí loại giỏi”.
A ∩ B là biến cố “Học sinh được chọn đạt điểm tổng kết loại giỏi cả hai môn Hóa học và Vật lí”.
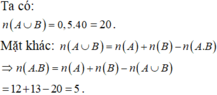

a) Xác suất để cả hai học sinh được chọn đều đạt yêu cầu là 93%. 87% = 0,8091
b) Xác suất để cả hai học sinh được chọn đều không đạt yêu cầu là
7%. 13% = 0,0091
c) Xác suất để chỉ có đúng một học sinh được chọn đạt yêu cầu là
93%.13% + 7%.87% = 0,1818
d) Xác suất để có ít nhất một trong hai học sinh được chọn đạt yêu cầu là
0,8091 + 0,1818 = 0,9909
a: Xác suất để cả hai học sinh được chọn đều đạt yêu cầu là:
\(0.93\cdot0.87=0.8091\)
b: Xác suất để cả hai người được chọn không đạt yêu cầu là:
(1-0,93)(1-0,87)=0,13*0,07=0,091
c: Xác suất để chỉ có 1 người đạt yêu cầu là:
0,93(1-0,87)+0,87(1-0,93)
=0,93*0,13+0,87*0,07
=0,1818
d: Để có ít nhất 1 trong 2 người đạt yêu cầu thì:
0,8091 + 0,1818 = 0,9909