Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y = a'x + b'\left( {a' \ne 0} \right)\) song song với nhau khi chúng không có điểm chung.
- Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y = a'x + b'\left( {a' \ne 0} \right)\) cắt nhau khi chúng có một điểm chung.
- Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y = a'x + b'\left( {a' \ne 0} \right)\) trùng nhau khi chúng có vô số điểm chung.

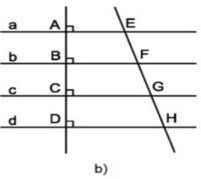
a) Các đường thẳng a, b, c, d song song cách đều ⇒ AB = BC = CD
⇒ B là trung điểm của AC; C là trung điểm của BD
- Hình thang AEGC (AE // GC) có B là trung điểm của AC và BF song song hai cạnh đáy
⇒ F là trung điểm EG (định lí đường trung bình của hình thang)
⇒ EF = FG
- Chứng minh tương tự ⇒ G là trung điểm FH
⇒ FG = GH
Vậy EF = FG = GH

Định lí:
+ Nếu các đường thẳng song song cách đều cắt một đường thằng thì chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau.
+ Nếu các đường thẳng song song cắt một đường thẳng và chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau thì chúng song song cách đều.
⇒ EF = FG = GH
Chọn đáp án C.

Định lí:
+ Nếu các đường thẳng song song cách đều cắt một đường thằng thì chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau.
+ Nếu các đường thẳng song song cắt một đường thẳng và chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau thì chúng song song cách đều.
⇒ EF = FG = GH
Chọn đáp án C.

Tương tự 1A
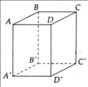
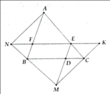
a) AB' và C'D song song, B'D' và AD chéo nhau, AC và A'C' song song.
b) BC' song song với (ADD'A').
c) AC' và CA' cắt nhau tại C.
d) (ACC'A') và (BDD'B') cắt nhau theo giao tuyến OO' (O và O' lần lượt là giao của AC, BD và A'C', B'D')

a) Vẽ đường thẳng y = 2x -1 trên mặt phẳng tọa độ
Với x = 0 thì y = -1, ta được điểm A(0; -1) thuộc đồ thị hàm số y = 2x – 1
Với x = 1 thì y = 1, ta được điểm B(1; 1) thuộc đường thẳng y = 2x – 1
Đồ thị hàm số y = 2x – 1 là một đường thẳng đi qua hai điểm A(0; -1) và điểm B(1; 1)
b) Vì đường thẳng y = ax + b \(\left( {a \ne 0} \right)\) song song với đường thẳng y = 2x -1 nên a = 2
Đường thẳng dã cho là: y = 2x + b
Vì đường thẳng y = 2x + b đi qua điểm M(1; 3) nên:
3 = 2.1 + b suy ra b = 1
Vậy đường thẳng cần tìm là; y = 2x + 1
* Vẽ đường thẳng y = 2x + 1
Với x = 0 thì y = 1, ta được điểm P(0, 1) thuộc đồ thị hàm số y = 2x + 1
Với x = 1 thì y = 1, ta được điểm Q(1; 3) thuộc đồ thị hàm số y = 2x + 1
Đồ thị hàm số y = 2x + 1 là đường thẳng đi qua hai điểm P(0; 1) và Q(1; 3)

a) Đúng
b) Sai
c) Đúng
d) Sai