Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án đúng là D
+ Xét điểm \(\left( {1;1} \right)\) ta có: \(y = - 5.1 + 5 = 0 \ne 1\). Do đó, điểm \(\left( {1;1} \right)\)không thuộc đồ thị hàm số.
+ Xét điểm \(\left( {2;0} \right)\) ta có: \(y = - 5.2 + 5 = - 5 \ne 0\). Do đó, điểm \(\left( {2;0} \right)\)không thuộc đồ thị hàm số.
+ Xét điểm \(\left( {0;4} \right)\) ta có: \(y = - 5.0 + 5 = 5 \ne 4\). Do đó, điểm \(\left( {0;4} \right)\)không thuộc đồ thị hàm số.
+ Xét điểm \(\left( {2; - 5} \right)\) ta có: \(y = - 5.2 + 5 = - 5\). Do đó, điểm \(\left( {2; - 5} \right)\) thuộc đồ thị hàm số.

Xét điểm \(M\left( { - 1; - 4} \right)\) ta có:
\(f\left( { - 1} \right) = 4.\left( { - 1} \right) = - 4\). Do đó, điểm \(M\left( { - 1; - 4} \right)\) thuộc vào đồ thị hàm số \(y = 4x\).
Xét điểm \(N\left( {1; - 4} \right)\) ta có:
\(f\left( 1 \right) = 4.1 = 4 \ne - 4\). Do đó, điểm \(N\left( {1; - 4} \right)\) không thuộc vào đồ thị hàm số \(y = 4x\).
Xét điểm \(P\left( {\dfrac{1}{4};1} \right)\) ta có:
\(f\left( {\dfrac{1}{4}} \right) = 4.\dfrac{1}{4} = 1\). Do đó, điểm \(P\left( {\dfrac{1}{4};1} \right)\) không thuộc vào đồ thị hàm số \(y = 4x\).

Baif2:
A=\(12x^2+20x-8+9\)
=\(4\left(3x^2+5x-2\right)+9\)
=4.0+9
= 9
vậy A=............
hc tốt
\(3x^2+5x-2=0\)
\(\Leftrightarrow3x^2-x+6x-2=0\)
\(\Leftrightarrow x\left(3x-1\right)+2\left(3x-1\right)=0\)
\(\Leftrightarrow\left(3x-1\right)\left(x+2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=-2\\x=\frac{1}{3}\end{cases}}\)

a) \(\left(x+1\right)\left(x^2-x+1\right)-\left(x-1\right)\left(x^2+x+1\right)\)
\(=\left(x^3+1\right)-\left(x^3-1\right)\)
\(=x^3+1-x^3+1\)
\(=2\)
Biểu thức trên có giá trị bằng 2 với mọi x nên không phụ thuộc vào biến.
b) \(\left(2x+3y\right)\left(4x^2-6xy+9y^2\right)-\left(2x-3y\right)\left(4x^2+6xy+9y^2\right)-27\left(2y^3-1\right)\)
\(=\left(8x^3+27y^3\right)-\left(8x^3-27y^3\right)-27\left(2y^3-1\right)\)
\(=8x^3+27y^3-8x^3+27y^3-54y^3+27\)
\(=27\)
Biểu thức trên có giá trị bằng 27 với mọi x nên không phụ thuộc vào biến.
c) \(\left(x-1\right)^3-\left(x+4\right)\left(x^2-4x+16\right)+3x\left(x-1\right)\)
\(=x^3-3x^2+3x-1-x^3-64+3x^2-3x\)
\(=-65\)
Biểu thức trên có giá trị bằng -65 với mọi x nên không phụ thuộc vào biến.
d) \(\left(x+y+z\right)^2+\left(x-y\right)^2+\left(x-z\right)^2+\left(y-z\right)^2-3\left(x^2+y^2+z^2\right)\)
\(=x^2+y^2+z^2+2\left(xy+yz+xz\right)+\left(x-y\right)^2+\left(x-z\right)^2+\left(y-z\right)^2-3\left(x^2+y^2+z^2\right)\)
\(=2\left(xy+yz+xz\right)-2\left(x^2+y^2+z^2\right)+x^2-2xy+y^2+x^2-2xz+z^2+y^2-2yz+z^2\)
\(=2\left(xy+yz+xz\right)-2\left(x^2+y^2+z^2\right)+2\left(x^2+y^2+z^2\right)-2\left(xy+yz+xz\right)\)
\(=0\)
Biểu thức trên có giá trị bằng 0 với mọi x nên không phụ thuộc vào biến.

Bài 1 :
a) \(\left(3x-1\right)^2-\left(3x+2\right)\left(3x-2\right)=2014\)
\(\Leftrightarrow9x^2-6x+1-\left(9x^2-4\right)=2014\)
\(\Leftrightarrow-6x=2009\)
\(\Leftrightarrow x=-\dfrac{2009}{6}=-334\dfrac{5}{6}\)
b) \(5x^2+4xy+4y^2+4x+1=0\)
\(\Leftrightarrow\left(x^2+4xy+4y^2\right)+\left(4x^2+4x+1\right)=0\)
\(\Leftrightarrow\left(x+2y\right)^2+\left(2x+1\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+2y=0\\2x+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=\dfrac{1}{4}\end{matrix}\right.\)
Bài 2 :
Ta có :
\(D=\left(4x^2-12xy+9y^2\right)-\left(9y^2-4\right)-\left(1-4x+4x^2\right)+12xy-4x\)
\(=4x^2-12xy+9y^2-9y^2+4-1+4x-4x^2+12xy-4x=3\)
Vậy biểu thức D không phụ thuộc vào các biến x,y

a) Ta có:
\(f\left( {\dfrac{1}{5}} \right) = \dfrac{5}{{4.\dfrac{1}{5}}} = \dfrac{5}{{\dfrac{4}{5}}} = 5:\dfrac{4}{5} = 5.\dfrac{5}{4} = \dfrac{{25}}{4};\)
\(f\left( { - 5} \right) = \dfrac{5}{{4.\left( { - 5} \right)}} = \dfrac{5}{{ - 20}} = \dfrac{{ - 1}}{4};\)
\(f\left( {\dfrac{4}{5}} \right) = \dfrac{5}{{4.\dfrac{4}{5}}} = \dfrac{5}{{\dfrac{{16}}{5}}} = 5:\dfrac{{16}}{5} = 5.\dfrac{5}{{16}} = \dfrac{{25}}{{16}}\)
b) Ta có:
\(f\left( { - 3} \right) = \dfrac{5}{{4.\left( { - 3} \right)}} = \dfrac{5}{{ - 12}} = \dfrac{{ - 5}}{{12}};\)
\(f\left( { - 2} \right) = \dfrac{5}{{4.\left( { - 2} \right)}} = \dfrac{5}{{ - 8}} = \dfrac{{ - 5}}{8};\)
\(f\left( { - 1} \right) = \dfrac{5}{{4.\left( { - 1} \right)}} = \dfrac{5}{{ - 4}} = \dfrac{{ - 5}}{4};\)
\(f\left( { - \dfrac{1}{2}} \right) = \dfrac{5}{{4.\left( { - \dfrac{1}{2}} \right)}} = \dfrac{5}{{\dfrac{{ - 4}}{2}}} = \dfrac{5}{{ - 2}} = \dfrac{{ - 5}}{2}\);
\(f\left( {\dfrac{1}{4}} \right) = \dfrac{5}{{4.\dfrac{1}{4}}} = \dfrac{5}{{\dfrac{4}{4}}} = \dfrac{5}{1} = 5\);
\(f\left( 1 \right) = \dfrac{5}{{4.1}} = \dfrac{5}{4}\);
\(f\left( 2 \right) = \dfrac{5}{{4.2}} = \dfrac{5}{8}\)
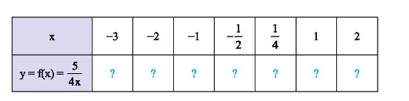
Ta có bảng sau:
\(x\) | –3 | –2 | –1 | \( - \dfrac{1}{2}\) | \(\dfrac{1}{4}\) | 1 | 2 |
\(y = f\left( x \right) = \dfrac{5}{{4x}}\) | \(\dfrac{{ - 5}}{{12}}\) | \(\dfrac{{ - 5}}{8}\) | \(\dfrac{{ - 5}}{4}\) | \(\dfrac{{ - 5}}{2}\) | 5 | \(\dfrac{5}{4}\) | \(\dfrac{5}{8}\) |

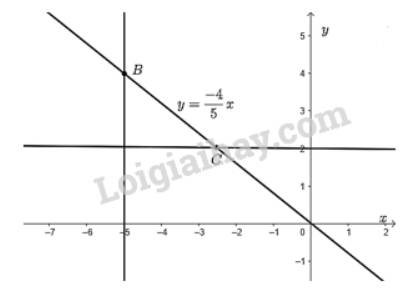
Từ điểm \(y = 2\) trên \(Oy\) vẽ đường thẳng vuông góc với \(Oy\) cắt đồ thị hàm số tại điểm \(C\). Khi đó, điểm \(C\) là điểm trên đồ thị hàm số có tung độ bằng 2.

a) Vì đồ thị hàm số đi qua điểm \(M\left( {1; - 2} \right)\)nên ta có:
\( - 2 = a.1 - 4 \Leftrightarrow a = - 2 + 4 = 2\)
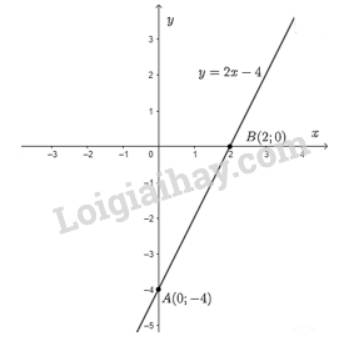
Hàm số cần tìm là \(y = 2x - 4\) có hệ số góc \(a = 2\).
b) Cho \(x = 0 \Rightarrow y = - 4\) ta được điểm \(A\left( {0; - 4} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{4}{2} = 2\) ta được điểm \(B\left( {2;0} \right)\) trên \(Ox\).
Đồ thị hàm số là đường thẳng đi qua hai điểm \(A\) và \(B\).
Đáp án đúng là D
+ Xét điểm \(\left( {1;1} \right)\) ta có: \(y = 2 - 4.1 = - 2 \ne 1\). Do đó, điểm \(\left( {1;1} \right)\)không thuộc đồ thị hàm số.
+ Xét điểm \(\left( {2;0} \right)\) ta có: \(y = 2 - 4.2 = - 6 \ne 2\). Do đó, điểm \(\left( {2;0} \right)\)không thuộc đồ thị hàm số.
+ Xét điểm \(\left( {1; - 1} \right)\) ta có: \(y = 2 - 4.1 = - 2 \ne - 1\). Do đó, điểm \(\left( {1; - 1} \right)\)không thuộc đồ thị hàm số.
+ Xét điểm \(\left( {1; - 2} \right)\) ta có: \(y = 2 - 4.1 = - 2\). Do đó, điểm \(\left( {1; - 2} \right)\) thuộc đồ thị hàm số.
Thế lần lượt chọn ý D