Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nhiệt lượng để nước đá để tăng lên 0oC
\(Q_2=m_2.c_2.\left(t-t_2\right)=6.2100.\left(0--20\right)=252000J\)
Nhiệt lượng nước tỏa ra để hạ xuống 0oC
\(Q_1=m_1.c_1.\left(t_1-t\right)=2.4200.\left(25-0\right)=210000J\)
Vì \(Q_1< Q_2\) nên có một lượng nước sẽ đông đặc. Gọi khối lượng nước đông đặc là \(m_3\), ta có phương trình cân bằng nhiệt:
\(252000=210000+340000m_3\)
\(\Leftrightarrow252000-210000=340000m_3\)
\(\Leftrightarrow42000=340000m_3\)
\(\Leftrightarrow m_3=\dfrac{4200}{3400000}\approx0,12kg\)
Vậy nhiệt độ sau khi cân bằng: \(0^oC\)
Lượng nước còn lại: \(2-0,12=1,88kg\)

nhiệt lượng cần thiết để tăng nước đá từ - 30 đến 0 là \(Q_1=1.2100.30=63000\left(J\right)\)
nhiệt lượng cần thiết để làm tan 1 kg đá là \(Q_2=1.34.10^4=340000\left(J\right)\)
Nhiệt lượng tỏa ra khi nước hạ từ 48 đến 0 là \(Q_3=2.4200.48=403200\left(J\right)\)
Vì \(Q_3>Q_2+Q_1\) nên đá tan hết, nhiệt đọ cân bằng lớn hơn 0
Nhiệt độ cân bằng của hỗn hợp là \(\text{⇔ m1c1 ( t1 − t ) = Q1 + Q2 + m2c1 ( t − t0 ) }\)
\(\text{⇔ 2.4200. ( 48 − t ) = 63000 + 340000 + 1.4200 ( t − 0 )}\)
\(\text{⇔ 8400 ( 48 − t ) = 403000 + 4200 t }\)
\(\text{⇔ 403200 − 8400 t = 403000 + 4200 t }\)
\(\text{⇔ 200 = 12600 t ⇒ t = 0 , 016^0C }\)

Đáp án: D
- Nhiệt lượng do nước đá thu vào để tan chảy hoàn toàn ở 0°C là:
![]()
- Nhiệt lượng do nước tỏa ra khi hạ xuống 0°C là:
![]()
- Ta thấy Q t h u > Q t ỏ a chứng tỏ chỉ 1 phần nước đá bị tan ra.
- Như vậy khi cân bằng nhiệt, hỗn hợp gồm cả nước và nước đá.
- Hay khi cân bằng nhiệt, nhiệt độ của hỗn hợp là t = 0 0 C

Đáp án: C
- Nhiệt lượng cần cung cấp cho 1,6kg nước đá thu vào để tăng nhiệt độ từ - 10 0 C lên 0 0 C :
![]()
- Nhiệt lượng nước đá thu vào để nóng chảy hoàn hoàn ở 0 0 C
![]()
- Nhiệt lượng do 2kg nước toả ra để hạ nhiệt độ từ 50 0 C đến 0 0 C
![]()
- Nhiệt lượng do nhiệt lượng kế bằng nhôm toả ra để hạ nhiệt độ từ 80 0 C xuống tới 0 0 C
![]()
- Ta có:
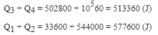
![]()
- Vì Q t h u > Q toả chứng tỏ nước đá chưa tan hết
- Nhiệt độ cuối cùng của hỗn hợp nước và nước đá cũng chính là nhiệt độ cuối cùng của nhiệt lượng kế và bằng 0 0 C

Tóm tắt:
m1 = 2kg
c1= 4200J/kg.K
t1 =48oC
m2 = 1kg
c2= 1800J/kg.K
t2 =-30oC
t=?
Giải:
Nhiệt độ cân bằng của hỗn hợp là:
Q1=Q2 (phương trình cân bằng nhiệt)
m1.c1.△t1=m2.c2.△t2
m1.c1.(t1-t)=m2.c2.(t-t2)
m1.c1.t1 - m1.c1.t = m2.c2.t - m2.c2.t2
m1.c1.t1 + m2.c2.t2 = m2.c2.t + m1.c1.t
m1.c1.t1 + m2.c2.t2 = t(m2.c2 + m1.c1)
t = \(\dfrac{m_1.c_1.t_1+m_2.c_2.t_2}{m_1.c_1+m_2.c_2}\)
t=\(\dfrac{2.4200.48+1.1800.\left(-30\right)}{2.4200+1.1800}\)\(\approx\)34,24oC
Đáp số : t \(\approx\)34,24oC

Đáp án: C
- Giả sử nhiệt độ của hỗn hợp sau khi cân bằng là 0 0 C
- Nhiệt lượng do nước tỏa ra khi hạ xuống 0 0 C là:
![]()
- Nhiệt lượng thu vào của viên nước đá để tăng nhiệt độ lên 0 0 C và tan hết tại 0 0 C là:
![]()
- Ta thấy Q t h u < Q t ỏ a chứng tỏ nước đá bị tan ra hoàn toàn.
- Gọi nhiệt độ hỗn hợp sau khi cân bằng là t 0 C (t > 0)
- Nhiệt lượng do nước tỏa ra khi hạ xuống 0 0 C là:
![]()
- Nhiệt lượng thu vào của viên nước đá để tăng nhiệt độ lên 0 0 C , tan hết tại 0 0 C và tăng lên đến t 0 C là:
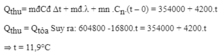
Tóm tắt:
\(m_1=2kg\)
\(m_2=30kg\)
\(t_1=25^oC\)
\(t_2=-20^oC\)
\(c_1=4200J/kg.K\)
\(c_2=2100J/kg.K\)
\(\lambda=340000J/kg\)
==========
\(t=?^oC\)
\(m_{\text{nước đá còn trong bình}}=?kg\)
Nhiệt lượng cần thiết để nước đá tăng lên 0oC:
\(Q_2=m_2.c_2.\left(t-t_2\right)=30.2100.\left(0--20\right)=1260000J\)
Nhiệt lượng cần thiết để nước giảm xuống 0oC
\(Q_1=m_1.c_1.\left(t_1-t\right)=2.4200.\left(25-0\right)=210000J\)
Vì \(Q_1< Q_2\) nên có một lượng nước sẽ bị đông đặc. Nên ta gọi khối lượng nước đông đặc là \(m_3\), ta có phương trình cân bằng nhiệt:
\(1260000=210000+340000m_3\)
\(\Leftrightarrow1260000-210000=340000m_3\)
\(\Leftrightarrow1050000=340000m_3\)
\(\Leftrightarrow m_3=\dfrac{1050000}{340000}\approx3,1kg\)
Vậy nhiệt độ nước sau khi cân bằng là \(0^oC\)
Khối lượng nước đá còn lại trong bình: \(m_{\text{nước đá còn trong bình}}=m_2+m_3=30+3,1=33,1kg\)
theo mình thấy thì chỉ có 2kg nước trong bình