Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: 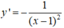
- Lấy điểm M(x0;y0) ∈ (C).
- Phương trình tiếp tuyến tại điểm M là:
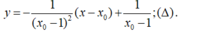
+ Giao với trục hoành: 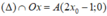
+ Giao với trục tung: 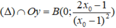
- Ta có:
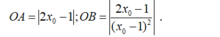
- Theo giả thiết tam giác OAB có diện tích bằng 2 nên:
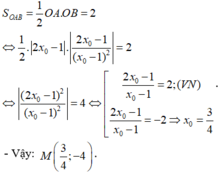

\(y'=\frac{-1}{\left(x-1\right)^2}\), gọi \(M\left(a;\frac{1}{a-1}\right)\)
Phương trình tiếp tuyến d qua M:
\(y=\frac{-1}{\left(a-1\right)^2}\left(x-a\right)+\frac{1}{a-1}\)
Gọi giao điểm của d với Ox và Oy lần lượt là A và B \(\Rightarrow\left\{{}\begin{matrix}A\left(2a-1;0\right)\\B\left(0;\frac{2a}{\left(a-1\right)^2}\right)\end{matrix}\right.\)
Do \(S_{OAB}=2\Rightarrow\frac{1}{2}OA.OB=2\Rightarrow OA.OB=4\)
\(\Rightarrow\left|\left(2a-1\right)\frac{2a}{\left(a-1\right)^2}\right|=4\Rightarrow\left\{{}\begin{matrix}\frac{2a\left(2a-1\right)}{\left(a-1\right)^2}=4\\\frac{2a\left(2a-1\right)}{\left(a-1\right)^2}=-4\end{matrix}\right.\) \(\Rightarrow a=\frac{2}{3}\)
\(\Rightarrow M\left(\frac{2}{3};-3\right)\)

Câu 2:
\(f'\left(x\right)=\frac{-3}{\left(2x-1\right)^2}\)
a/ \(x_0=-1\Rightarrow\left\{{}\begin{matrix}f'\left(x_0\right)=-\frac{1}{3}\\f\left(x_0\right)=0\end{matrix}\right.\)
Pttt: \(y=-\frac{1}{3}\left(x+1\right)=-\frac{1}{3}x-\frac{1}{3}\)
b/ \(y_0=1\Rightarrow\frac{x_0+1}{2x_0-1}=1\Leftrightarrow x_0+1=2x_0-1\Rightarrow x_0=2\)
\(\Rightarrow f'\left(x_0\right)=-\frac{1}{3}\)
Pttt: \(y=-\frac{1}{3}\left(x-2\right)+1\)
c/ \(x_0=0\Rightarrow\left\{{}\begin{matrix}f'\left(x_0\right)=-3\\y_0=-1\end{matrix}\right.\)
Pttt: \(y=-3x-1\)
d/ \(6x+2y-1=0\Leftrightarrow y=-3x+\frac{1}{2}\)
Tiếp tuyến song song d \(\Rightarrow\) có hệ số góc bằng -3
\(\Rightarrow\frac{-3}{\left(2x_0-1\right)^2}=-3\Rightarrow\left(2x_0-1\right)^2=1\Rightarrow\left[{}\begin{matrix}x_0=0\Rightarrow y_0=-1\\x_0=1\Rightarrow y_0=2\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}y=-3x-1\\y=-3\left(x-1\right)+2\end{matrix}\right.\)
Làm câu 1,3 trước, câu 2 hơi dài tối rảnh làm sau:
1/ \(\lim\limits\frac{n^2+2n+1}{2n^2-1}=lim\frac{1+\frac{2}{n}+\frac{1}{n^2}}{2-\frac{1}{n^2}}=\frac{1}{2}\)
\(\lim\limits_{x\rightarrow0}\frac{2\sqrt{x+1}-x^2+2x+2}{x}=\frac{2-0+0+2}{0}=\frac{4}{0}=+\infty\)
Chắc bạn ghi nhầm đề, câu này biểu thức tử số là \(...-x^2+2x-2\) thì hợp lý hơn
3/ \(y'=2sin2x.\left(sin2x\right)'=4sin2x.cos2x=2sin4x\)
b/ \(y'=4x^3-4x\)
c/ \(y'=\frac{3\left(x+2\right)-1\left(3x-1\right)}{\left(x+2\right)^2}=\frac{7}{\left(x+2\right)^2}\)
d/ \(y'=10\left(x^2+x+1\right)^9\left(x^2+x+1\right)'=10\left(x^2+x+1\right)^9.\left(2x+1\right)\)
e/ \(y'=\frac{\left(2x^2-x+3\right)'}{2\sqrt{2x^2-x+3}}=\frac{4x-1}{2\sqrt{2x^2-x+3}}\)


- Ta có :
Lấy điểm M ( x 0 ; y 0 ) ∈ C .
+ Phương trình tiếp tuyến tại điểm M là:
+ Giao với trục hoành:
+ Giao với trục tung:
- Ta có:
- Theo giả thiết tam giác OAB có diện tích bằng 2 nên:
Chọn D