QT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
Ta có: \({u_n} - {u_{n - 1}} = \left( {2n - 1} \right) - \left[ {2\left( {n - 1} \right) - 1} \right] = 2\)
Vậy dãy số \(\left( {{u_n}} \right)\) là cấp số cộng với \({u_1} = 2 \times 1 - 1 = 1,\;\;\;d = 2\)
\({S_{100}} = \frac{{100}}{2}\left[ {2 \times 1 + \left( {100 - 1} \right).2} \right] = 10\;000\)
Chọn đáp án C.
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Ta có: 3; – 6; 12; – 24; ... là cấp số nhân với u1 = 3 và công bội q = – 2.
Khi đó tổng của 12 số hạng đầu của cấp số nhân đã cho là:
\({S_{12}} = \frac{{3\left[ {1 - {{\left( { - 2} \right)}^{12}}} \right]}}{{1 - \left( { - 2} \right)}} = 12\,\,285\).
b) Ta có: \(\frac{1}{{10}},\frac{1}{{100}},\frac{1}{{1\,\,000}},...\) là một cấp số nhân với u1 = \(\frac{1}{{10}}\) và công bội \(q = \frac{1}{{10}}\)
Khi đó tổng của 5 số hạng đầu của cấp số nhân đã cho là:
\({S_5} = \frac{{\frac{1}{{10}}\left[ {1 - {{\left( {\frac{1}{{10}}} \right)}^5}} \right]}}{{1 - \frac{1}{{10}}}} = 0,1111\).
HQ
Hà Quang Minh
Giáo viên
25 tháng 8 2023
a, Ta có thể sắp xếp 50 số tự nhiên chẵn đầu tiên thành cấp số cộng có số hạng đầu \(u_1=0\) và công sai \(d=2\)
b, Giả sử cấp số cộng có số hạng đầu \(u_1\) và công sai d.
Ta có:
\(u_3+u_{28}=\left(u_1+2d\right)+\left(u_1+27d\right)=2u_1+29d\Leftrightarrow2u_1+29d=100\\ \Rightarrow S_{30}=\dfrac{30\cdot\left[2u_1+29d\right]}{2}=\dfrac{30\cdot100}{2}=1500\)
c, Giả sử cấp số cộng có số hạng đầu \(v_1\) và công sai \(d\)
Ta có:
\(S_6=18\Leftrightarrow\dfrac{6\cdot\left[2v_1+5d\right]}{2}=18\Leftrightarrow2v_1+5d=6\left(1\right)\\ S_{10}=110\Leftrightarrow\dfrac{10\cdot\left[2v_1+9d\right]}{2}=110\Leftrightarrow2v_1+9d=22\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}2v_1+5d=6\\2v_1+9d=22\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}v_1=-7\\d=4\end{matrix}\right.\)
\(\Rightarrow S_{20}=\dfrac{20\cdot\left[2v_1+19d\right]}{2}=\dfrac{20\cdot\left[2\cdot\left(-7\right)+19\cdot4\right]}{2}=620\)
AH
Akai Haruma
Giáo viên
14 tháng 3 2018
Lời giải:
Gọi công sai là $d$. Nếu \(-2,x,6,y\) là một cấp số cộng thì:
\(\left\{\begin{matrix} x=-2+d(1)\\ 6=x+d(2)\\ y=6+d(3)\end{matrix}\right.\)
Từ \((1);(2)\Rightarrow 6=x+d=-2+2d\Rightarrow d=4\)
\((1)\Rightarrow x=-2+4=2\)
\((3)\Rightarrow y=6+4=10\)
Do đó đáp án D
CM
17 tháng 12 2017
Rõ ràng trong hộp có 30 quả với 15 quả ghi số chẵn, 10 quả màu đỏ, 5 quả màu đỏ ghi số chẵn, 25 quả màu xanh hoặc ghi số lẻ. Vậy theo định nghĩa
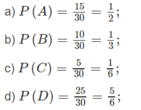
Trong đó A, B, C, D là các biến cố tương ứng với các câu a), b), c) ,d).
AH
Akai Haruma
Giáo viên
26 tháng 10 2018
Lời giải:
a) Chọn một đội gồm $12$ người từ $15+10=25$ người có số cách chọn là: \(C^{12}_{25}\)
b) Bạn xem lại đề.
LT
3 tháng 4 2017
a) 1110 – 1 = (1 + 10)10 – 1 = (1 + C110 10 + C210102 + … +C910 109 + 1010) – 1
= 102 + C210102 +…+ C910 109 + 1010.
Tổng sau cùng chia hết cho 100 suy ra 1110 – 1 chia hết cho 100.
b) Ta có
101100 – 1 = (1 + 100)100 - 1
= (1 + C1100 100 + C2100 1002 + …+C99100 10099 + 100100) – 1.
= 1002 + C21001002 + …+ 10099 + 100100.
Tổng sau cùng chia hết cho 10 000 suy ra 101100 – 1 chia hết cho 10 000.
c) (1 + √10)100 = 1 + C1100 √10 + C2100 (√10)2 +…+ (√10)99 + (√10)100
(1 - √10)100 = 1 - C1100 √10 + C2100 (√10)2 -…- (√10)99 + (√10)100
√10[(1 + √10)100 – (1 - √10)100] = 2√10[C1100 √10 + C3100 (√10)3 +…+ . (√10)99]
= 2(C1100 10 + C3100 102 +…+ 1050)
Tổng sau cùng là một số nguyên, suy ra √10[(1 + √10)100 – (1 - √10)100] là một số nguyên.
BT
23 tháng 5 2017
a) \(11^{10}-1=\left(10+1\right)^{10}-1\)\(=C^0_{10}10^{10}+C^1_{10}10^9+...+C^9_{10}10+C^{10}_{10}-1\)
\(=10^{10}+C^1_{10}10^9+...+C^8_{10}10^2+10.10\) chia hết cho 100.
b) \(\left(101\right)^{100}-1=\left(100+1\right)^{100}-1\)
\(=100^{100}+C_{100}^{99}100^{99}+....+C^1_{100}100+C_{100}^{100}100^0-1\)
\(=100^{100}+C_{100}^{99}100^{99}+....+C^2_{100}100^2+100.100+1-1\)
\(=100^{100}+C_{100}^{99}100^{99}+....+C^2_{100}100^2+10000\) chia hết cho 10000.
Đáp án đúng là: A
Các số tự nhiên lẻ lập thành một cấp số cộng với số hạng đầu u1 = 1 và công sai d = 2.
Do đó tổng 100 số hạng đầu tiên của cấp số cộng này là:
\({S_{100}} = \frac{{100.\left( {1 + 1 + 99.2} \right)}}{2} = 10\,000\).