K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LL
1
31 tháng 1 2022
\(B=10101\cdot\left(\dfrac{5}{111111}+\dfrac{5}{222222}-\dfrac{4}{111111}\right)\)
\(=10101\cdot\left(\dfrac{2}{222222}+\dfrac{5}{222222}\right)\)
\(=10101\cdot\dfrac{1}{31746}=\dfrac{7}{22}\)
NB
9 tháng 8 2019
10101 . \(\left(\frac{5}{111111}+\frac{5}{222222}-\frac{4}{3.7.11.13.37}\right)\)
= 10101 . \(\left(\frac{5}{111111}+\frac{5}{222222}-\frac{4}{111111}\right)\)
= 10101 . \(\frac{7}{222222}\)
= \(\frac{7}{22}\)
Z
9 tháng 8 2019
Lời giải:
Ta có:
\(A=10101.\left(\frac{5}{111111}+\frac{5}{222222}-\frac{4}{3.7.11.13.37}\right)\)
\(=10101.\left(\frac{5}{111111}+\frac{5}{222222}-\frac{4}{111111}\right)\)
\(=10101.\left(\frac{10}{222222}+\frac{5}{222222}-\frac{8}{222222}\right)\)
\(=10101.\left(\frac{10+5-8}{222222}\right)\)
\(=10101.\frac{7}{222222}\)
\(=\frac{7.10101}{22.10101}=\frac{7}{22}\)
Chúc bạn học tốt!
Tick cho mình nhé!
27 tháng 1 2016
A = 1.2.3+23.1.2.3+33.1.2.3+43.1.2.3 /3.4.5+23.3.4.5+33.3.4.5+43.3.4.5
=1.2.3 (1+23+33+43)/3.4.5 (1+23+33+43)
=1.2.3/3.4.5
=1/10
B=10101 ( 15/333333 + 2/333333 +57 / 333333 )
B=10101 . 74 /333333
=74/33
27 tháng 1 2016
bai....................kho......................wa.....................troi.........................thi.................lanh...............lai....................mua...................tich....................ung.....................ho..................minh....................nha.......................huhu
12 tháng 7 2023
b: \(=8.2\left(11+\dfrac{94}{1591}-6-\dfrac{38}{1517}\right):\left(8+\dfrac{11}{43}\right)\)
\(=\dfrac{41}{5}\cdot\left(5+\dfrac{60}{1763}\right):\dfrac{355}{43}\)
\(=\dfrac{41}{5}\cdot\dfrac{8875}{1763}\cdot\dfrac{43}{355}\)
\(=5\)
c: \(=10101\cdot\left(\dfrac{10+5}{222222}-\dfrac{4}{111111}\right)\)
\(=10101\cdot\dfrac{7}{222222}=\dfrac{7}{22}\)
H
1
16 tháng 6 2015
\(B=1-\frac{1}{1+2}-\frac{1}{1+2+3}-...-\frac{1}{1+2+3+...+2016}\)
\(=1-\left(\frac{1}{1+2}+\frac{1}{1+2+3}+...+\frac{1}{1+2+3+...+2016}\right)\)
\(=1-\left(\frac{1}{2.3:2}+\frac{1}{3.4:2}+...+\frac{1}{2016.2017:2}\right)\)
\(=1-\left(\frac{2}{2.3}+\frac{2}{3.4}+....+\frac{2}{2016.2017}\right)\)
\(=1-2\left(\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{2016.2017}\right)\)
\(=1-2\left(\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{2016}-\frac{1}{2017}\right)\)
\(=1-2\left(\frac{1}{2}-\frac{1}{2017}\right)=1-\left(1-\frac{2}{2017}\right)=1-1+\frac{2}{2017}=\frac{2}{2017}\)
8 tháng 7 2021
a)Xét \(\Delta ABI\)vuông tại A và \(\Delta KBI\)vuông tại K ,có:
\(\widehat{ABI}=\widehat{KBI}\)(do BI là phân giác của \(\widehat{ABC}\))
\(BI:chung\)
\(\Rightarrow\Delta ABI=\Delta KBI\left(ch.gn\right)\)
b)Vì \(\Delta ABI=\Delta KBI\left(ch.gn\right)\)
\(\Rightarrow\hept{\begin{cases}AB=KB\\AI=BI\end{cases}}\)(2 cạnh tương ứng)
\(\Rightarrow B,I\)thuộc đường trung trực của AK
hay BI là đường trung trực của AK
c)Vì BI là phân giác của \(\widehat{ABC}\)
\(\Rightarrow\)\(\widehat{ABI}=\widehat{KBI}=\frac{\widehat{ABC}}{2}=\frac{60^0}{2}=30^0=\widehat{ACB}\)(do \(\Delta ABC\)vuông tại A)
\(\Rightarrow\Delta BIC\)cân tại I
mà IK là đường cao
\(\Rightarrow IK\)là đường trung tuyến của \(\Delta BIC\)
\(\Rightarrowđpcm\)
9 tháng 7 2021
//Sorry bạn nha .Hôm qua chỗ mình mưa to quá lại còn có sấm sét nữa nên mình không giải tiếp được cho bạn .
c)Vì \(\Delta BIC\)cân tại I nên IB=IC
Xét \(\Delta ABI\)vuông tại A ,có:
\(IB\)là cạnh huyền
\(\Rightarrow AB< IB=IC\)
d)Vì \(\Delta ABC\)vuông tại A \(\Rightarrow AB\perp AC\)
Xét \(\Delta BIC\),có:
BA,IK,CF là các đường cao
\(\Rightarrow BA,IK,CF\)đồng quy tại trực tâm của \(\Delta BIC\)
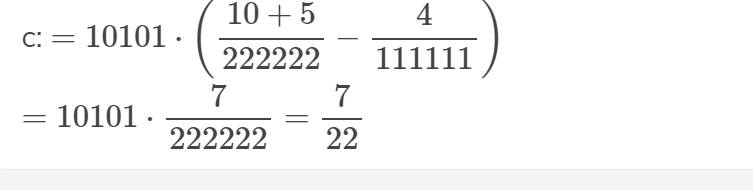
Bài làm
\(\sqrt{111111+222222+333333}\)
\(=\sqrt{666666}\)
\(=\sqrt{3^2.74074}\)
=> \(3\sqrt{74074}\)
# Học tốt #