Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khi cộng hai hỗn số 315;223315;223 bạn Cường làm như sau:
315+223=165+83=4815+4015=8815=51315315+223=165+83=4815+4015=8815=51315
a)Bạn Cường đã tiến hành cộng hai hỗn số như thế nào?
b)Có cách nào tính nhanh hơn không?
Giải
a)Bạn Cường đã đổi hỗn số thành phân số rồi cộng hai phân số, cuối cùng đổi kết quả thành hỗn số.
b)Có thể cộng hai phần nguyên với nhau, hai phần phân số với nhau:
Tổng hai phần nguyên là: 3 + 2 = 5.
Tổng hai phần phân số là : 15+23=3+1015=131515+23=3+1015=1315
Vậy 315+223=51315315+223=51315.
a) Bạn Cường đã đổi tất cả các hỗn số ra phân số rồi cộng chúng lại.
b) Cách nhanh hơn:
\(3\dfrac{1}{5}+2\dfrac{2}{3}=\left(3+2\right)+\left(\dfrac{1}{5}+\dfrac{2}{3}\right)\)
=5+\(\dfrac{13}{15}\)
=\(5\dfrac{13}{15}\)

a,
= \(\dfrac{20}{100}.\dfrac{15}{36}-\)(\(\dfrac{2}{5}+\dfrac{2}{3}\)):\(\dfrac{6}{5}\)
= \(\dfrac{20.15}{100.36}\)- ( \(\dfrac{6}{15}+\dfrac{10}{15}\)): \(\dfrac{6}{5}\)
= \(\dfrac{1.5}{5.12}-\dfrac{16}{15}:\dfrac{6}{5}\)
= \(\dfrac{1.1}{1.12}-\dfrac{16.5}{10.6}\)
= \(\dfrac{1}{12}-\dfrac{16.1}{2.6}\)
= \(\dfrac{1}{12}\) - \(\dfrac{16}{12}\)
= \(\dfrac{1}{12}+\dfrac{\left(-16\right)}{12}\)
= \(\dfrac{15}{12}\) = \(\dfrac{5}{4}\)
b,
= \(\dfrac{6}{7}+\dfrac{5}{4}+\dfrac{\left(-4\right)}{7}+\dfrac{25}{4}\)
= (\(\dfrac{6}{7}+\dfrac{\left(-4\right)}{7}\)) + (\(\dfrac{5}{4}+\dfrac{25}{4}\))
= \(\dfrac{2}{7}+\dfrac{30}{4}\)
= \(\dfrac{2}{7}+\dfrac{15}{2}\)
= \(\dfrac{4}{14}+\dfrac{105}{14}\)
= \(\dfrac{109}{14}\)

a) \(\dfrac{1}{6};\dfrac{1}{3};\dfrac{1}{2};...\)
\(\Rightarrow\dfrac{1}{6};\dfrac{2}{6};\dfrac{3}{6};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{4}{6}\)
b) \(\dfrac{1}{8};\dfrac{5}{24};\dfrac{7}{24};...\)
\(\Rightarrow\dfrac{3}{24};\dfrac{5}{24};\dfrac{7}{24};...\)
Dãy có quy luật tăng dần lên 2 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{9}{24}\)
c) \(\dfrac{1}{5};\dfrac{1}{4};\dfrac{1}{3};...\)
\(\dfrac{4}{20};\dfrac{5}{20};\dfrac{6}{20};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{7}{20}\)
d) \(\dfrac{4}{15};\dfrac{3}{10};\dfrac{1}{3};...\)
\(\Rightarrow\dfrac{8}{30};\dfrac{9}{30};\dfrac{11}{30};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{12}{30}\)

a)\(\dfrac{-36}{63};\dfrac{56}{63};\dfrac{-30}{63}\)
b)\(\dfrac{110}{264};\dfrac{21}{264}\)

a)\(\dfrac{3}{10}\)-x=\(\dfrac{25}{30}\)-\(\dfrac{4}{30}\)
\(\dfrac{3}{10}-x=\dfrac{7}{10}\)
x = \(\dfrac{3}{10}-\dfrac{7}{10}\)
x=\(\dfrac{-4}{10}\)
b)\(\dfrac{-5}{8}+x=\dfrac{4}{9}-\dfrac{63}{9}\)
\(\dfrac{-5}{9}+x=\dfrac{-59}{9}\)
\(x=\dfrac{-59}{9}-\dfrac{-5}{9}\)
\(x=\dfrac{-64}{9}\)
c)=>2.18=(x-3).(x-3)
=>36=(x-3)\(^2\)
=>6\(^2\)=(x-3)\(^2\)
6= x-3
x=6+3=9

hực hiện phép nhân hoặc phép chia hai hỗn số bằng cách viết hỗn số dưới dạng phân số:
a) 512.334512.334 b) 613:429613:429
Giải
a) 512.334=112.154=1658;512.334=112.154=1658;
b) 6{1 \over 3}:4{2 \over 9} = {{19} \over 3}:{{38} \over 9} = {{19} \over 3}.{9 \over {38}} = {3 \over 2}\)
Lưu ý: Khi cộng hai hỗn số ta có thể cộng phần nguyên với nhau, phần phân số với nhau. Nhưng nhân (hoặc chia) hai hỗn số ta không thể nhân (hoặc chia) phần nguyên với nhau và phần phân số với nhau.


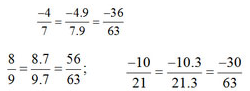
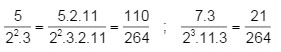
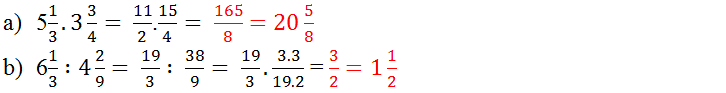
a) \(5\dfrac{7}{10}.15=\dfrac{57}{10}.15=\dfrac{57}{2.5}.3.5=\dfrac{171}{2}=85\dfrac{1}{2}\)
b) \(4\dfrac{2}{5}:2=\left(4+\dfrac{2}{5}\right):2=2+\dfrac{1}{5}=\dfrac{11}{5}=2\dfrac{1}{5}\)
a) \(5\dfrac{7}{10}.15=\left(5+\dfrac{7}{10}\right).15=5.15+\dfrac{7}{10}.15=75+\dfrac{21}{2}=75+10+\dfrac{1}{2}=85+\dfrac{1}{2}=85\dfrac{1}{2}=\dfrac{171}{2}\)
b)
\(\left(4\dfrac{2}{5}\right):2=\left(4+\dfrac{2}{5}\right):2=\left(4:2\right)+\left(\dfrac{2}{5}:2\right)=2+\dfrac{1}{5}=2\dfrac{1}{5}=\dfrac{11}{5}\)