Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(A=\dfrac{1}{3}+\dfrac{1}{6}+\dfrac{1}{10}+\dfrac{1}{15}+\dfrac{1}{21}+...+\dfrac{1}{300}\)
\(=\dfrac{2}{6}+\dfrac{2}{12}+\dfrac{2}{20}+\dfrac{2}{30}+\dfrac{2}{42}+...+\dfrac{2}{600}\)
\(=\dfrac{2}{2.3}+\dfrac{2}{3.4}+\dfrac{2}{4.5}+\dfrac{2}{5.6}+\dfrac{2}{6.7}+...+\dfrac{2}{24.25}\)
\(=2\left(\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+...+\dfrac{1}{24.25}\right)\)
\(=2\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{24}-\dfrac{1}{25}\right)\)
\(=2\left(\dfrac{1}{2}-\dfrac{1}{25}\right)\)
\(=2\cdot\dfrac{23}{50}=\dfrac{23}{25}\)
Vậy A = \(\dfrac{23}{25}\).
It's very easy :)))))
Call expression is A, we have:
\(A=\dfrac{1}{3}+\dfrac{1}{6}+\dfrac{1}{10}+\dfrac{1}{15}+\dfrac{1}{21}+...+\dfrac{1}{300}.\)
\(\Rightarrow2A=2\left(\dfrac{1}{3}+\dfrac{1}{6}+\dfrac{1}{10}+\dfrac{1}{15}+\dfrac{1}{21}+...+\dfrac{1}{300}\right).\)
\(\Rightarrow2A=\dfrac{2}{6}+\dfrac{2}{12}+\dfrac{2}{20}+\dfrac{2}{30}+\dfrac{2}{42}+...+\dfrac{2}{600}.\)
\(\Rightarrow2A=\dfrac{2}{2.3}+\dfrac{2}{3.4}+\dfrac{2}{4.5}+\dfrac{2}{5.6}+\dfrac{2}{6.7}+...+\dfrac{2}{24.25}.\)
\(\Rightarrow2A=2\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+...+\dfrac{1}{24}-\dfrac{1}{25}\right).\)
\(\Rightarrow2A=2\left(\dfrac{1}{2}-\dfrac{1}{25}\right).\)
\(\Rightarrow2A=2\left(\dfrac{25}{50}-\dfrac{2}{50}\right).\)
\(\Rightarrow2A=2.\dfrac{23}{50}=\dfrac{23}{25}.\)
Vậy.....

Nếu:
\(\dfrac{a}{b}< 1\Rightarrow\dfrac{a+n}{b+n}< 1\left(n\in N\right)\)
\(B=\dfrac{10^{20}+1}{10^{21}+1}< 1\)
\(B< \dfrac{10^{20}+1+9}{10^{21}+1+9}\Rightarrow B< \dfrac{10^{20}+10}{10^{21}+10}\Rightarrow B< \dfrac{10\left(10^{19}+1\right)}{10\left(10^{20}+1\right)}\Rightarrow B< \dfrac{10^{19}+1}{10^{20}+1}=A\)\(\Rightarrow B< A\)

\(A=\dfrac{1}{10}+\dfrac{1}{15}+\dfrac{1}{21}+...+\dfrac{1}{120}\)
\(A=\dfrac{2}{20}+\dfrac{2}{30}+\dfrac{2}{42}+...+\dfrac{2}{240}\)
\(A=\dfrac{2}{4.5}+\dfrac{2}{5.6}+\dfrac{2}{6.7}+...+\dfrac{2}{15.16}\)
\(A=2\left(\dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+...+\dfrac{1}{15.16}\right)\)
\(A=2\left(\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+...+\dfrac{1}{15}-\dfrac{1}{16}\right)\)
\(A=2\left(\dfrac{1}{4}-\dfrac{1}{16}\right)\)
\(A=2.\dfrac{3}{16}\)
\(A=\dfrac{3}{8}\)
\(B=\dfrac{4}{3.7}+\dfrac{4}{7.11}+\dfrac{4}{11.15}+...+\dfrac{4}{107.111}\)
\(B=\dfrac{1}{3}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{15}+...+\dfrac{1}{107}-\dfrac{1}{111}\)
\(B=\dfrac{1}{3}-\dfrac{1}{111}\)
\(B=\dfrac{12}{37}\)

\(\dfrac{1}{2}N=\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{9.10}\)
\(\dfrac{1}{2}N=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{9}-\dfrac{1}{10}\)
\(\dfrac{1}{2}N=\dfrac{1}{2}-\dfrac{1}{10}=\dfrac{2}{5}\)
N=\(\dfrac{2}{5}:\dfrac{1}{2}=\dfrac{4}{5}\)

\(B=\dfrac{1}{10}+\dfrac{1}{15}+\dfrac{1}{21}+...+\dfrac{1}{120}\)
\(\Leftrightarrow B=\dfrac{2}{20}+\dfrac{2}{30}+\dfrac{2}{42}+...+\dfrac{2}{240}\)
\(\Leftrightarrow B=2\left(\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+...+\dfrac{1}{240}\right)\)
\(\Leftrightarrow B=2\left(\dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+...+\dfrac{1}{15.16}\right)\)
\(\Leftrightarrow B=2\left(\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+...+\dfrac{1}{15}-\dfrac{1}{16}\right)\)
\(\Leftrightarrow B=2\left(\dfrac{1}{4}-\dfrac{1}{16}\right)=\dfrac{3}{8}\)
Vì \(\dfrac{3}{8}< \dfrac{1}{2}\)
\(\Rightarrow B< \dfrac{1}{2}\left(ĐPCM\right)\)

Thay dấu ba chấm bởi x rồi tìm x.
Chẳng hạn:
\(a) \) \(\dfrac{7}{9}-\dfrac{x}{3}=\dfrac{1}{9}\)
\(\Rightarrow\dfrac{x}{3}=\dfrac{7}{9}-\dfrac{1}{9}\)
\(\Rightarrow\dfrac{x}{3}=\dfrac{6}{9}=\dfrac{2}{3}\)
Vậy x = 2
Đáp số:
a) x = 2
b) x = 3
c) x = 7
d) x =19.

\(\dfrac{1}{10}+\dfrac{1}{15}+\dfrac{1}{21}+...+\dfrac{1}{120}\)
\(=\dfrac{2}{20}+\dfrac{2}{30}+\dfrac{2}{42}+...+\dfrac{2}{240}\)
\(=2\times\left(\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+...\dfrac{1}{240}\right)\)
\(=2\times\left(\dfrac{1}{4\times5}+\dfrac{1}{5\times6}+\dfrac{1}{6\times7}+...+\dfrac{1}{15\times16}\right)\)
\(=2\times\left(\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+...+\dfrac{1}{15}-\dfrac{1}{16}\right)\)
\(=2\times\left(\dfrac{1}{4}-\dfrac{1}{16}\right)\)
\(=\dfrac{3}{8}\)
=2/20+2/30+2/42+.....+2/240
=2/4.5+2/5.6+2/6.7+.....+2/15.16
=1/2[1/4.5+1/5.6+1/6.7+.....+1/15.16]
=1.2[1/4-1/5+1/5-1/6+.....+1/15-1/16]
=1/2[1/4-1/16]
=1/2.3/16
=3/32

1 )Ta có
\(M=\left(\dfrac{1}{2^2}-1\right)\cdot\left(\dfrac{1}{3^2}-1\right)\cdot\left(\dfrac{1}{4^2}-1\right)...\left(\dfrac{1}{100^2}-1\right)\)
\(=\left(\dfrac{1}{2}-1\right)\left(\dfrac{1}{2}+1\right)\left(\dfrac{1}{3}-1\right)\left(\dfrac{1}{3}+1\right).....\left(\dfrac{1}{100}-1\right)\left(\dfrac{1}{100}+1\right)\)
\(=\dfrac{-1}{2}\cdot\dfrac{3}{2}\cdot\dfrac{-2}{3}\cdot\dfrac{4}{3}\cdot\dfrac{-3}{4}\cdot\dfrac{5}{4}\cdot\cdot\cdot\cdot\dfrac{-99}{100}\cdot\dfrac{101}{100}\)
\(=\dfrac{-1\cdot\left(-2\right)\cdot\left(-3\right)\cdot3\cdot\left(-4\right)\cdot4\cdot\left(-5\right)\cdot5....\cdot\left(-100\right)\cdot100\cdot101}{2^2\cdot3^2\cdot4^2....\cdot100^2}\)
\(=-\dfrac{101}{200}< \dfrac{1}{2}\)
2 ) Số phân số của biểu thức B là 180 phân số
Ta có
\(\dfrac{1}{20}>\dfrac{1}{200};\dfrac{1}{21}>\dfrac{1}{200};\dfrac{1}{22}>\dfrac{1}{200};....;\dfrac{1}{199}>\dfrac{1}{200}\)
\(\Rightarrow B=\dfrac{1}{20}+\dfrac{1}{21}+...+\dfrac{1}{200}>\dfrac{1}{200}\cdot180=\dfrac{9}{10}\)

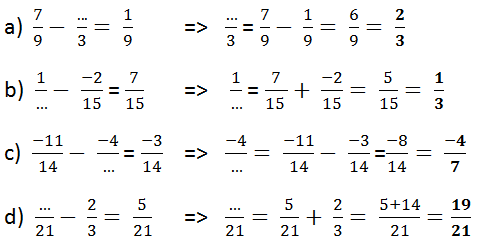
\(S=\dfrac{1}{10}+\dfrac{1}{15}+\dfrac{1}{21}+...+\dfrac{1}{300}\)
\(S=\dfrac{2}{20}+\dfrac{2}{30}+\dfrac{2}{42}+...+\dfrac{2}{600}\)
\(S=\dfrac{2}{4.5}+\dfrac{2}{5.6}+\dfrac{2}{6.7}+...+\dfrac{2}{24.25}\)
\(S=2.(\dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+...+\dfrac{1}{24.25})\)
\(S=2.(\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+...+\dfrac{1}{24}-\dfrac{1}{25})\)
\(S=2.(\dfrac{1}{4}-\dfrac{1}{25})\)
\(S=2.\dfrac{21}{100}\)
\(S=\dfrac{21}{50}\)
\(\Rightarrow S=\dfrac{21}{50}\)
S = \(\dfrac{1}{10}\) + \(\dfrac{1}{15}+\dfrac{1}{21}+...+\dfrac{1}{300}\)
S = \(\dfrac{2}{20}+\dfrac{2}{30}+\dfrac{2}{42}+...+\dfrac{2}{600}\)
S = \(\dfrac{2}{4.5}+\dfrac{2}{5.6}+\dfrac{2}{6.7}+...+\dfrac{2}{24.25}\)
S = 2 (\(\dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+...+\dfrac{1}{24.25}\))
S = 2 (\(\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+...+\dfrac{1}{24}-\dfrac{1}{25}\))
S = 2 . (\(\dfrac{1}{4}-\dfrac{1}{25}\))
S = 2 . \(\dfrac{21}{100}\)
=> S = \(\dfrac{21}{50}\)