Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A=a2sin90∘+b2cos90∘+c2cos180∘A=a2sin90∘+b2cos90∘+c2cos180∘
=a2*1+b2* 0 +c2* (-1
=a2 - c2
B=3−sin290∘+2cos260∘−3tan245∘B=3−sin290∘+2cos260∘−3tan245∘.
= 3 - 1 + 1/2 - 3 = -1/2


1234567890-01234567890-=qưertyuiop[]\';;lkjhfgdsazxcvbnm,./\'l;[]7894561230.+-

a) Ta có A=\dfrac{\tan \alpha+3 \dfrac{1}{\tan \alpha}}{\tan \alpha+\dfrac{1}{\tan \alpha}}=\dfrac{\tan ^{2} \alpha+3}{\tan ^{2} \alpha+1}=\dfrac{\dfrac{1}{\cos ^{2} \alpha}+2}{\dfrac{1}{\cos ^{2} \alpha}}=1+2 \cos ^{2} \alphaA=tanα+tanα1tanα+3tanα1=tan2α+1tan2α+3=cos2α1cos2α1+2=1+2cos2α Suy ra A=1+2 \cdot \dfrac{9}{16}=\dfrac{17}{8}A=1+2⋅169=817.
b) B=\dfrac{\dfrac{\sin \alpha}{\cos ^{3} \alpha}-\dfrac{\cos \alpha}{\cos ^{3} \alpha}}{\dfrac{\sin ^{3} \alpha}{\cos ^{3} \alpha}+\dfrac{3 \cos ^{3} \alpha}{\cos ^{3} \alpha}+\dfrac{2 \sin \alpha}{\cos ^{3} \alpha}}=\dfrac{\tan \alpha\left(\tan ^{2} \alpha+1\right)-\left(\tan ^{2} \alpha+1\right)}{\tan ^{3} \alpha+3+2 \tan \alpha\left(\tan ^{2} \alpha+1\right)}B=cos3αsin3α+cos3α3cos3α+cos3α2sinαcos3αsinα−cos3αcosα=tan3α+3+2tanα(tan2α+1)tanα(tan2α+1)−(tan2α+1).
Suy ra B=\dfrac{\sqrt{2}(2+1)-(2+1)}{2 \sqrt{2}+3+2 \sqrt{2}(2+1)}=\dfrac{3(\sqrt{2}-1)}{3+8 \sqrt{2}}B=22+3+22(2+1)2(2+1)−(2+1)=3+823(2−1).

a) Vì 90^{\circ}<\alpha<180^{\circ}90∘<α<180∘ nên \cos \alpha<0cosα<0 mặt khác \sin ^{2} \alpha+\cos ^{2} \alpha=1sin2α+cos2α=1 suy ra \cos \alpha=-\sqrt{1-\sin ^{2} \alpha}=-\sqrt{1-\dfrac{1}{9}}=-\dfrac{2 \sqrt{2}}{3}cosα=−1−sin2α=−1−91=−322.
Do đó \tan \alpha=\dfrac{\sin \alpha}{\cos \alpha}=\dfrac{\dfrac{1}{3}}{-\dfrac{2 \sqrt{2}}{3}}=-\dfrac{1}{2 \sqrt{2}}tanα=cosαsinα=−32231=−221.
b) Vì \sin ^{2} \alpha+\cos ^{2} \alpha=1sin2α+cos2α=1 nên \sin \alpha=\sqrt{1-\cos ^{2} \alpha}=\sqrt{1-\dfrac{4}{9}}=\dfrac{\sqrt{5}}{3}sinα=1−cos2α=1−94=35 và \cot \alpha=\dfrac{\cos \alpha}{\sin \alpha}=\dfrac{-\dfrac{2}{3}}{\dfrac{\sqrt{5}}{3}}=-\dfrac{2}{\sqrt{5}}cotα=sinαcosα=35−32=−52.
c) Vì \tan \gamma=-2 \sqrt{2}<0 \Rightarrow \cos \alpha<0tanγ=−22<0⇒cosα<0 mặt khác \tan ^{2} \alpha+1=\dfrac{1}{\cos ^{2} \alpha}tan2α+1=cos2α1 nên \cos \alpha=-\sqrt{\dfrac{1}{\tan ^{2}+1}}=-\sqrt{\dfrac{1}{8+1}}=-\dfrac{1}{3}cosα=−tan2+11=−8+11=−31.
Ta có \tan \alpha=\dfrac{\sin \alpha}{\cos \alpha} \Rightarrow \sin \alpha=\tan \alpha \cdot \cos \alpha=-2 \sqrt{2} \cdot\left(-\dfrac{1}{3}\right)=\dfrac{2 \sqrt{2}}{3}tanα=cosαsinα⇒sinα=tanα⋅cosα=−22⋅(−31)=322 \Rightarrow \cot \alpha=\dfrac{\cos \alpha}{\sin \alpha}=\dfrac{-\dfrac{1}{3}}{\dfrac{2 \sqrt{2}}{3}}=-\dfrac{1}{2 \sqrt{2}}⇒cotα=sinαcosα=322−31=−221.

Tam giác ABC vuông tại B nên ta có: \(\tan C = \frac{{AB}}{{CB}} \Leftrightarrow AB = \tan {32^ \circ }.(1 + x)\)
Tam giác ADB vuông tại B nên ta có: \(\tan D = \frac{{AB}}{{DB}} \Leftrightarrow AB = \tan {40^ \circ }.x\)
\(\begin{array}{l} \Rightarrow \tan {32^ \circ }.(1 + x) = \tan {40^ \circ }.x\\ \Leftrightarrow x.(\tan {40^ \circ } - \tan {32^ \circ }) = \tan {32^ \circ }\\ \Leftrightarrow x = \frac{{\tan {{32}^ \circ }}}{{\tan {{40}^ \circ } - \tan {{32}^ \circ }}}\\ \Leftrightarrow x \approx 2,9\;(km)\end{array}\)
\( \Rightarrow AB \approx \tan {40^ \circ }.2,92 \approx 2,45\;(km)\)
Vậy chiều cao của ngọn núi là 2,45 km.

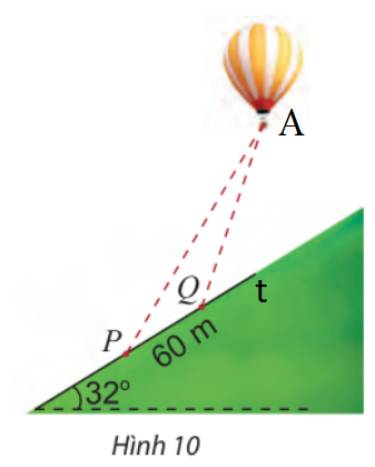
Gọi A là vị trí của khinh khí cầu, Pt là đường sườn đồi như hình.
Ta có:
Tại P, góc nâng của khinh khí cầu là \({62^ \circ }\)\( \Rightarrow \widehat P = {62^ \circ } - {32^ \circ } = {30^ \circ }\)
Tại Q, góc nâng của khinh khí cầu là \({70^ \circ }\)\( \Rightarrow \widehat {AQt} = {70^ \circ } - {32^ \circ } = {38^ \circ }\)
\( \Rightarrow \widehat {AQP} = {180^ \circ } - {38^ \circ } = {142^ \circ }\) và \(\widehat A = {180^ \circ } - {142^ \circ } - {30^ \circ } = {8^ \circ }\)
Áp dụng định lí sin trong tam giác APQ, ta có:
\(\begin{array}{l}\frac{{PQ}}{{\sin A}} = \frac{{QA}}{{\sin P}}\\ \Rightarrow QA = \sin P.\frac{{PQ}}{{\sin A}} = \sin {30^ \circ }.\frac{{60}}{{\sin {8^ \circ }}} \approx 215,56\;(m)\end{array}\)
Vậy khoảng cách từ Q đến khinh khí cầu là 215,56 m.

Áp dụng định lí cosin trong tam giác ABC, ta có:
\(\begin{array}{l}{c^2} = {b^2} + {a^2} - 2ab\cos C\\ \Leftrightarrow {c^2} = 26,{4^2} + 49,{4^2} - 2.26,4.49,4\cos {47^ \circ }20'\\ \Rightarrow c \approx 37\end{array}\)
Áp dụng định lí sin, ta có: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}\)
\(\begin{array}{l} \Leftrightarrow \frac{{49,4}}{{\sin A}} = \frac{{26,4}}{{\sin B}} = \frac{{37}}{{\sin {{47}^ \circ }20'}}\\ \Rightarrow \sin A = \frac{{49,4.\sin {{47}^ \circ }20'}}{{37}} \approx 0,982 \Rightarrow \widehat A \approx {79^ \circ }\\ \Rightarrow \widehat B \approx {180^ \circ } - {79^ \circ } - {47^ \circ }20' = {53^ \circ }40'\end{array}\)

Do a, b, c là độ dài 3 cạnh của tam giác ABC nên \(a+b-c\ne0\). Như vậy, \(\dfrac{a^3+b^3-c^3}{a+b-c}=c^2\)
\(\Leftrightarrow a^3+b^3-c^3=c^2a+c^2b-c^3\)
\(\Leftrightarrow a^3+b^3-c^2a-c^2b=0\)
\(\Leftrightarrow\left(a+b\right)\left(a^2-ab+b^2\right)-c^2\left(a+b\right)=0\)
\(\Leftrightarrow\left(a+b\right)\left(a^2-ab+b^2-c^2\right)=0\)
\(\Leftrightarrow a^2-ab+b^2-c^2=0\) (do \(a+b\ne0\))
\(\Leftrightarrow c^2=a^2+b^2-ab\) (1)
Mặt khác, theo định lý cosin, ta có \(c^2=a^2+b^2-2ab.\cos C\) (2)
Từ (1) và (2), ta thu được \(2\cos C=1\Leftrightarrow\cos C=\dfrac{1}{2}\Leftrightarrow\widehat{C}=60^o\)
Vậy \(\widehat{C}=60^o\)

a) Ta có: \(sin^2x+sin^2\left(90-x\right)=sin^2x+cos^2x=1.\)
áp dụng: A = 2
b)Ta có: \(cos\left(x\right)=-cos\left(180-x\right)\)
áp dụng: B = 0
c) Ta có: \(tan\left(x\right)\cdot tan\left(90-x\right)=\frac{sinx}{cosx}\cdot\frac{sin\left(90-x\right)}{cos\left(90-x\right)}=\frac{sinx}{cosx}\cdot\frac{cosx}{sinx}=1\)
áp dụng: C = 1
quá sai