Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo đề bài ta có:
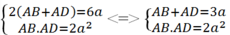
Coi AB và Ad như là các ẩn thì chungsex là các nghiệm của phương trình bậc hai:
![]()
(Tìm hai số khi biết tổng và tích của chúng).
Giải phương trình bận hai này ta có:
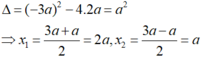
AB = 2a VÀ d = A (vì AB>AD)


Hướng dẫn trả lời:
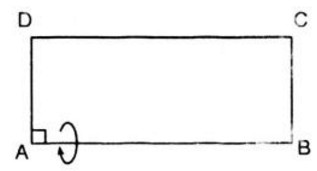
Theo đề bài ta có:
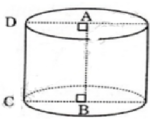
Diện tích hình chữ nhật ABCD là: AB.AD = 2a2 (1)
Chu vi hình chữ nhật là: 2(AB + CD) = 6a ⇒ AB + CD = 3a (2)
Từ (1) và (2), ta có AB và CD là nghiệm của phương trình:
x2 – 3ax – 2a2 = 0
Giải phương trình ta được x1 = 2a; x2 = a
Theo giả thiết AB > AD nên ta chọn AB = 2a; AD = a
Vậy diện tích xung quanh hình trụ là:
Sxq = 2π . AD . AB = 2π . a . 2a = 4 πa2
Thể tích hình trụ là:
V = π . AD2 . AB = π. a2 . 2a = 2πa3

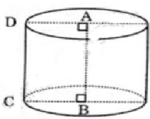
Theo đề bài ta có: AB + AD = 3a ; AB.AD = 2 a 2
Độ dài AB và AD là nghiệm của phương trình : x 2 – 3ax +2 a 2 = 0
∆ = (-3 a 2 ) - 4.1.2 a 2 = 9 a 2 – 8 a 2 = a 2 > 0
∆ = a 2 = a
x 1 = (3a +a)/2 = 2a ; x 2 = (3a -a)/2 = a
Vì AB > AD nên AB =2a ,AD =a
Diện tích xung quanh của hình trụ :
S = 2πrh = 2π.AD.AB = 2π.a.2a = 4π a 2 (đvdt)
Thể tích của hình trụ :
V = π. R 2 .h = π. A D 2 .AB = π. a 2 .2a = 2π. a 3 (đvdt)

Theo đề bài ta có: AB + AD = 3a ; AB.AD = 2a2
Độ dài AB và AD là nghiệm của phương trình : x2 – 3ax +2a2 = 0
Δ = (-3a2) - 4.1.2a2 = 9a2 – 8a2 = a2 > 0
√Δ = √a2 = a
x1 = (3a +a)/2 = 2a ; x2 = (3a -a)/2 = a
Vì AB > AD nên AB =2a ,AD =a
Diện tích xung quanh của hình trụ :
S = 2πrh = 2π.AD.AB = 2π.a.2a = 4πa2 (đvdt)
Thể tích của hình trụ :
V = π.R2.h = π.AD2.AB = π.a2.2a = 2π.a3 (đvdt)
Theo đề bài ta có: AB + AD = 3a ; AB.AD = 2a2
Độ dài AB và AD là nghiệm của phương trình :
x2 – 3ax +2a2 = 0 Δ = (-3a2) - 4.1.2a2 = 9a2 – 8a2 = a2 > 0 √Δ = √a2 = a x1 = (3a +a)/2 = 2a ; x2 = (3a -a)/2 = a

Ta có: S t p = 2 πBC . AB + 2 πBC 2 = 2 π . 2 a . a + 2 πa 2 = 6 πa 2
Ta có: V = π . BC 2 . AB = πa 2 . 2 a = 2 πa 3