Tính diện tích xung quanh, diện tích toàn phân của các lăng trụ đứng sau đây (h.102) :

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

SG

Sách Giáo Khoa

24 tháng 4 2017

Tính diện tích xung quanh, diện tích toàn phân của các lăng trụ đứng sau đây (h.102) :

1

LT

Lê Thiên Anh

24 tháng 4 2017

Giải bài 23 trang 111 SGK Toán 8 Tập 2 | Giải toán lớp 8

Các câu hỏi dưới đây có thể giống với câu hỏi trên

SG

Sách Giáo Khoa

24 tháng 4 2017

Tính diện tích xung quanh, diện tích toàn phần của các hình chóp tứ giác đều sau đây (h.126)

1

QD

Quốc Đạt

24 tháng 4 2017

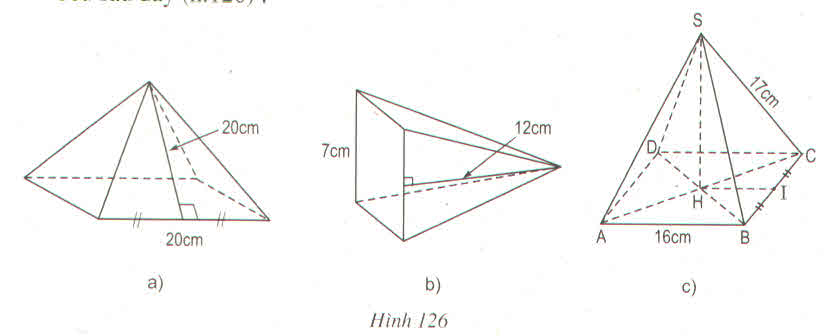
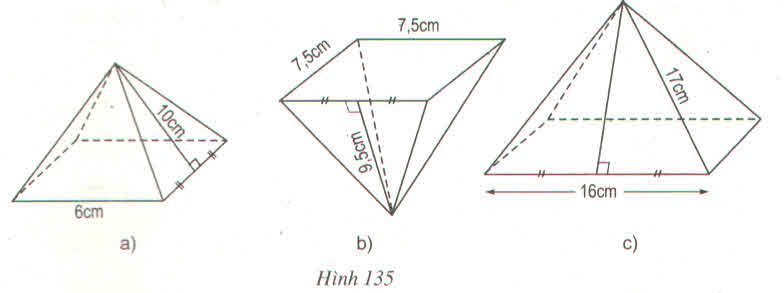
Hình a : S_xq = p.d = \(\dfrac{1}{2}\).20.4.20 = 800(cm²)

Diện tích đáy: S_đ = 20² = 400(cm²)

Diện tích toàn phần của lăng trụ hai là:

S_tp = S_xq + S_đ = 800 + 400 = 1200(cm²)

Hình b: S_xq = p.d = \(\dfrac{1}{2}\).7.4.12 = 168(cm²)

S_đ = 7² = 49(cm²)

S_tp = S_xq + S_đ = 168 + 49 = 217(cm²)

Hình c: Chiều cao của mặt bên của hình chóp:

\(h=\sqrt{17^2-8^2}=\sqrt{225}=15\left(cm\right)\)

S_xq = p.d = \(\dfrac{1}{2}\).16.4.15 = 480(cm²)

S_đ = 16² = 256(cm²)

S_tp = S_xq + S_đ = 480 + 256 = 736(cm²)

SG

Sách Giáo Khoa

6 tháng 5 2017

Tính diện tích toàn phần của lăng trụ đứng theo các kích thước cho ở hình 158 ?

2

TQ

Trần Quốc Chiến

10 tháng 5 2017

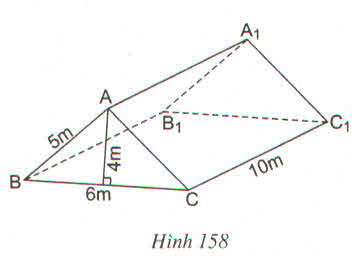
Diện tích đáy ABC: S₁= 1/2.6.4=12 (m²)

Diện tích mặt BCC₁B₁: S₂=6.10=60 (m²⁾

Diện tích AA₁C₁C: S₃₌10.5=50 (m²)

Ta thấy hai mặt AA₁B₁B và AA₁C₁C bằng nhau nên:

S_tp= 2S₁+S₂+2S₃= 2.12+60+2.50= 184 (m²)

NT

Nguyen Thuy Hoa

5 tháng 7 2017

Hình lăng trụ đứng. Hình chóp đều.

SG

Sách Giáo Khoa

6 tháng 5 2017

Tính thể tích và diện tích toàn phần của các hình lăng trụ đứng có các kích thước như hình 140 ?

1

NT

Nguyen Thuy Hoa

5 tháng 7 2017

Hình lăng trụ đứng. Hình chóp đều.

SG

Sách Giáo Khoa

6 tháng 5 2017

Cho các hình lăng trụ đứng với các kích thước như ở các hình 117 a), b), c)

a) Hãy tìm diện tích xung quanh của mỗi hình

b) Hãy tìm diện tích toàn phần của mỗi hình

1

KT

Kim Tuyến

17 tháng 4 2018

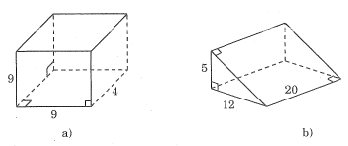
Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

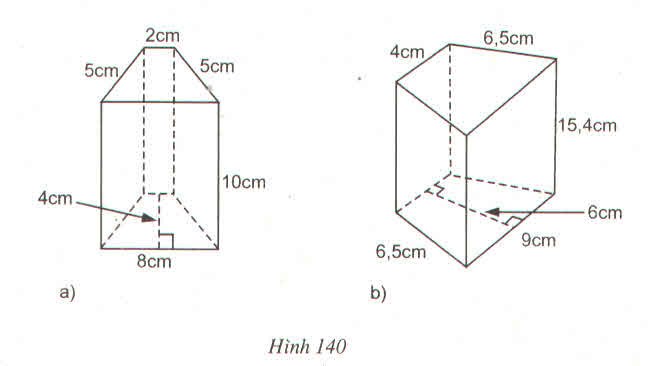
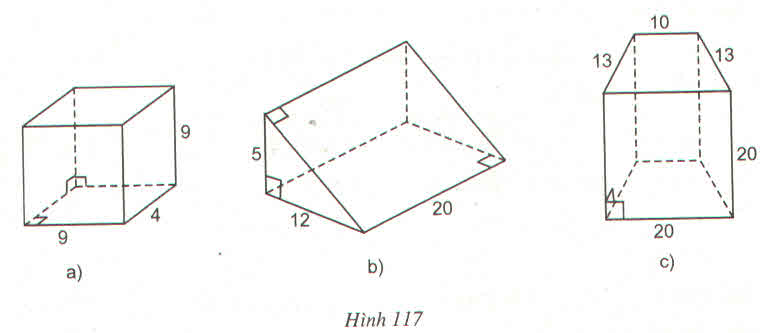
*Hình a:

Diện tích xung quanh là:(9 + 4) . 2 .9 = 284 (đơn vị diện tích)

Diện tích mặt đáy là: 9 . 4 = 36 (đơn vị diện tích)

Diện tích toàn phần: 234 + 36 . 2 = 306 (đơn vị diện tich)

*Hình b.

Áp dụng định lí Pi-ta-go, ta có: 5\(^2\) + 12\(^2\)= 25 + 144 = 169

Suy ra cạnh huyền của tam giác vuông bằng 13.

Diện tích xung quanh là: (5 + 12 + 13) . 20 = 600(đvdt)

Diện tích mặt đáy là: 1/2 .5.12 = 30 (đvdt)

Diện tích toàn phần là: 600 + 30 . 2 = 660(đvdt)

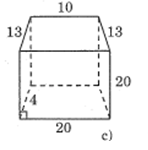
*Hình c: Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

Diện tích xung quanh là: (18 + 10 + 13 + 20).20 = 1120(đvdt)

Hình c có đáy là một hình thang cân từ đáy nhỏ kẻ 2 đường thẳng vuông góc với đáy lớn, ta được một hình chữ nhật có cạnh bằng 10 nên 2 phần còn lại đáy lớn bằng nhau và bằng 5.

Áp dụng định lí Pi-ta-go, ta có:

13\(^2\) - 5\(^2\)=169-25 =144

Chiều cao hình thang là 12.

Diện tích đáy là: (10-20)/2 .12 = 180 (đvdt)

Diện tích toàn phần là1120 + 180.2 = 1480 (đvdt)

SG

Sách Giáo Khoa

6 tháng 5 2017

Tìm diện tích toàn phần và thể tích của lăng trụ đứng có các kích thước như ở hình 164.

2

TC

Trọng Chi Ca Vâu

12 tháng 5 2017

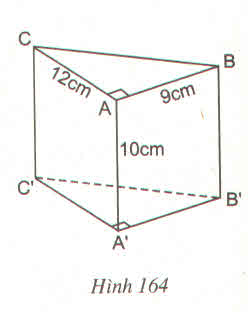
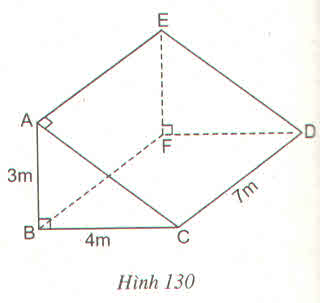
áp dụng định lí Py-ta-go vào \(\Delta\)ABC vuông tại A:

BC=\(\sqrt{AB^2+AC^2}\)=\(\sqrt{9^2+12^2}\)=15(cm)

S_xq=(12+9+15).10=360(cm²)

Sđ=12.9:2=54(cm²)

S_tp=S_xq+2Sđ=360+2.54=468(cm²)

V=Sđ.h=54.10=540(cm³)

NT

Nguyen Thuy Hoa

5 tháng 7 2017

Hình lăng trụ đứng. Hình chóp đều.

SG

Sách Giáo Khoa

24 tháng 4 2017

Tính diện tích xung quanh của các hình chóp tứ giác đều sau đây (h.135)

1

QD

Quốc Đạt

24 tháng 4 2017

Hình a: S_xq = p.d = \(\dfrac{1}{2}\).6.4. 10 = 120(cm²)

Hình b: S_xq = p.d = \(\dfrac{1}{2}\).7,5 .4. 9,5 =142,5(cm²)

Hình c: Độ dài trung đoạn:

\(d=\sqrt{17^2-8^2}=\sqrt{289-64}=\sqrt{225}=15\left(cm\right)\)

Nên S_xq = p.d = \(\dfrac{1}{2}\).16.4.15 =480(cm²)

SG

Sách Giáo Khoa

6 tháng 5 2017

Đáy của lăng trụ đứng là một hình thang cân có các cạnh b = 11mm, a = 15mm và chiều cao \(h_r=7mm\) (h.127). Chiều cao của lăng trụ là \(h=14mm\).

Tính diện tích xung quanh của lăng trụ ?

1

LT

le thien hien vinh

12 tháng 6 2017

diện tích xung quanh của lăng trụ là (\(\sqrt{53}\times2+11+15)\)\(\times\)14\(\approx\)567,8mm²

SG

Sách Giáo Khoa

6 tháng 5 2017

Tìm diện tích toàn phần của hình lăng trụ đứng (theo các kích thước đã cho trên hình 130)

1

NL

Nguyễn Lê Phước Thịnh

17 tháng 5 2022

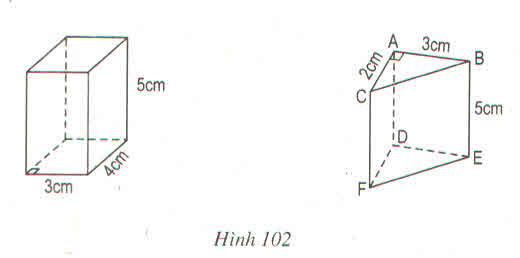
\(AC=\sqrt{3^2+4^2}=5\left(cm\right)\)

\(S_{XQ}=\left(AB+BC+AC\right)\cdot CD=84\left(cm^2\right)\)

\(S_{TP}=84+2\cdot6=96\left(cm^2\right)\)

SG

Sách Giáo Khoa

6 tháng 5 2017

Tính thể tích (theo các kích thước) của các hình lăng trụ đứng sau đây (h.135)

1

NL

Nguyễn Lê Phước Thịnh

17 tháng 5 2022

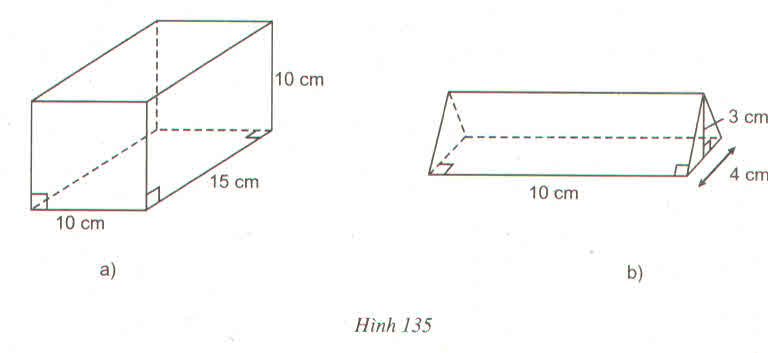
a: \(V=s\cdot h=10\cdot15\cdot10=1500\left(cm^3\right)\)

b: \(S_{Đáy}=\dfrac{1}{2}\cdot3\cdot4=6\left(cm^2\right)\)

\(V=S\cdot h=6\cdot10=60\left(cm^2\right)\)