Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)Vì AM là đường trung tuyền nên ta có
AM=1/2BC
AM=(1/2).5 => AM=2,5(cm)
b)áp dụng định lý Pytago vào tam giác ABC vuông tại A ta có
AB^2+AC^2=BC^2
thay số ta có : 3^2+AC^2=5^2=>9+AC^2=25=>AC^2=25-9=16
=>AC= căn bậc 2 của 16
=>AC=4(cm)
diện tích tam giác ABC là:
S=1/2a.h=1/2.3.4=6(cm2)
Hết nhé ^_^
ta có tam giác ABC vuông tại A
Áp dụng tỉ số lượng giác trong .........................
=> AM2=BM.BC
=>AM=\(\sqrt{2,5\times5}\approx3,6cm\)
diện tích tam giác vuông ABC là
STAM GIÁC ABC=\(\frac{1}{2}AM.BC=9cm^2\)

Giải:
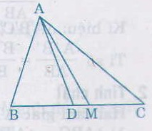
Ta có AD là đường phân giác của ∆ ABC nên
SABDSADCSABDSADC = ABACABAC = mnmn(kết quả ở bài 16)
=> SABDSADC+SABDSABDSADC+SABD= mn+mmn+m
hay SABDSABCSABDSABC= mn+mmn+m => SABMSABM= 1212 SABCSABC.
Giả sử AB < AC( m<n) vì AD là đường phân giác, AM là đường trung tuyến kẻ từ A nên AD nằm giữa AB và AM.
=> SADMSADM= SABMSABM - SABDSABD
=> SADMSADM = 1212S -mn+mmn+mS =
a)
Có AB < AC (vì n > m) (1)
Ta có: \(\dfrac{AB}{AC}=\dfrac{BD}{DC}\) ( vì AD là phân giác của góc BAC) (2)
Từ (1) và (2), ta có BD < CD
⇒ D nằm giữa B và M
Đặt S1, S2 lần lượt là diện tích △ADM và △ADC
Ta có: \(\dfrac{S_1}{S_2}=\dfrac{\dfrac{1}{2}.BD.AH}{\dfrac{1}{2}.CD.AH}=\dfrac{BD}{CD}=\dfrac{AB}{AC}=\dfrac{m}{n}\)
⇒ \(\dfrac{S_1+S_2}{S_2}=\dfrac{m+n}{n}=\dfrac{S}{S_2}=\dfrac{m+n}{n}\Rightarrow S_2=\dfrac{n.S}{m+n}\)
Vì \(S_{AMC}=S_{AMB}=\dfrac{1}{2}.S\Rightarrow\)diện tích của △ADM là
\(S_{ADM}=S_{ADC}-S_{AMC}=S_2-\dfrac{1}{2}.S=\dfrac{n.S}{m+n}-\dfrac{1}{2}.S=\left[\dfrac{n-m}{2\left(m+n\right)}\right].S\)
b)
\(S_{ADM}=\left[\dfrac{7-3}{2\left(7+3\right)}\right].S=\dfrac{2}{10}.S=\dfrac{1}{5}.S=0,2.S=20\%.S\)
Vậy diện tích của △ADM bằng 20% diện tích của △ABC

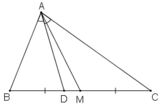
a) Ta có: 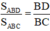 (do hai tam giác có chung chiều cao từ đỉnh A)
(do hai tam giác có chung chiều cao từ đỉnh A)
ΔABC có AD là phân giác
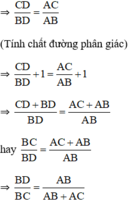
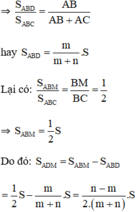
b) Với n = 7; m = 3, thay vào kết quả phần a ta có:
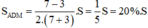
Vậy diện tích tam giác ADM chiếm 20% diện tích tam giác ABC.