
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 14)
\(a,\\ =-\dfrac{3}{8}+\dfrac{8}{17}+\dfrac{-5}{8}-\dfrac{3}{5}+\dfrac{9}{17}\\ =\left(\dfrac{-3}{8}+\dfrac{-5}{8}\right)+\left(\dfrac{8}{17}+\dfrac{9}{17}\right)-\dfrac{3}{5}\\ =\left(-1\right)+1-\dfrac{3}{5}=0-\dfrac{3}{5}=\dfrac{-3}{5}\\ b,\\ =\dfrac{7}{15}.\dfrac{-15}{14}+\left(\dfrac{27}{16}-\dfrac{1}{8}\right):\dfrac{5}{8}\)
\(=\dfrac{-1}{2}+\dfrac{25}{16}.\dfrac{8}{5}=\dfrac{-1}{2}+\dfrac{5}{2}=2\\ c,\\ =\dfrac{2}{2}-\dfrac{2}{3}+\dfrac{2}{3}-\dfrac{2}{4}+.....+\dfrac{2}{99}-\dfrac{2}{100}\\ =1-\dfrac{1}{50}=\dfrac{49}{50}\)
Câu 15
\(a,2x+\dfrac{-1}{4}=\dfrac{3}{2}\\ 2x=\dfrac{3}{2}-\dfrac{-1}{4}=\dfrac{7}{4}\\ x=\dfrac{7}{4}:2=\dfrac{7}{8}\\ b,\dfrac{15}{x}=\dfrac{-3}{4}\\ x=\dfrac{15.4}{-3}=-20\)

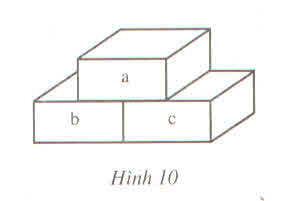
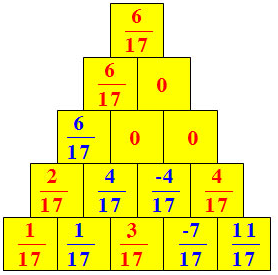
Làm theo quy tắc ở hình 10, ta có thể "xây tường" như sau:

Trên tia AB có: AC=10cm
}\(\Rightarrow\) AB>AC(vì 20>10)
AB= 20 cm
\(\Rightarrow\)Điểm C nằm giữa 2 điểm A Và B
Ta có : AC + AD = AB
hay 10 + AD = 20
AD= 20-10
AD=10
b) vì C nằm giữa 2 điểm A và B (câu a)và AC=AD=10 cm
\(\Rightarrow\) Điểm C là trung điểm của đoạn thẳng AB
Bài này đơn giản mà =))
Ta có: AC+BC=AB
Mà AB=20cm; AC=10cm => BC =10cm.
=> AC=BC=10cm
Mà C nằm giữa A và B => C là trung điểm AB.


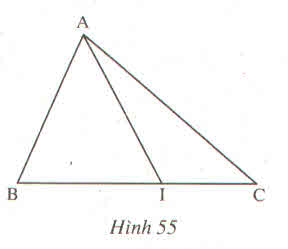
Giải:
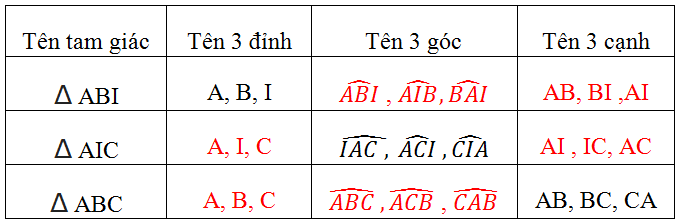
|
Tên tam giác |
Tên 3 đỉnh |
Tên 3 góc |
Tên 3 cạnh |
|
|
A,B,I |
|
AB, BI, IA |
|
|
A,I,C |
|
AI, IC, CA |
|
|
A,B,C |
|
AB, BC, CA |
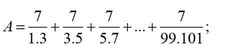
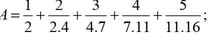



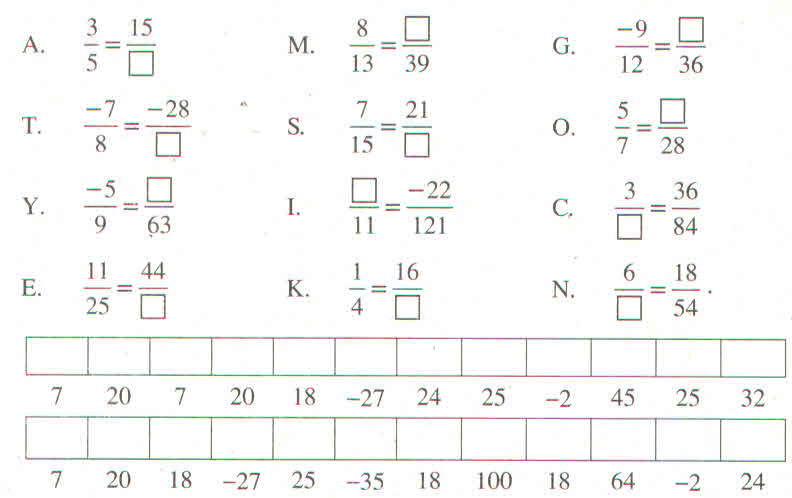
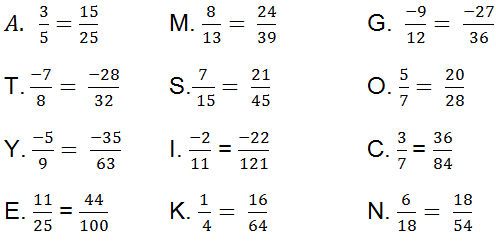

 mọi người làm bài 2 bài 3 giúp em với ạ (em cảm ơn)
mọi người làm bài 2 bài 3 giúp em với ạ (em cảm ơn) ;
;




1) A=\(\dfrac{7}{1.3}+\dfrac{7}{3.5}+\dfrac{7}{5.7}+...+\dfrac{7}{99.101}\)=\(\dfrac{7.2}{1.3.2}+\dfrac{7.2}{3.5.2}+\dfrac{7.2}{5.7.2}+...+\dfrac{7.2}{99.101.2}\)=
\(\dfrac{7}{2}\left(\text{}\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{99.101}\right)\)=
\(\dfrac{7}{2}\left(\text{}1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}...+\dfrac{1}{99}-\dfrac{1}{101}\right)\)=
\(\dfrac{7}{2}\left(\text{}1-\dfrac{1}{101}\right)\)=\(\dfrac{7}{2}.\dfrac{100}{101}=\dfrac{350}{101}\)
2) A=\(\dfrac{1}{2}+\dfrac{2}{2.4}+\dfrac{3}{4.7}+\dfrac{4}{7.11}+\dfrac{5}{11.16}\)=\(\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{16}\)
=\(\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{16}\)=\(1-\dfrac{1}{16}=\dfrac{15}{16}\)