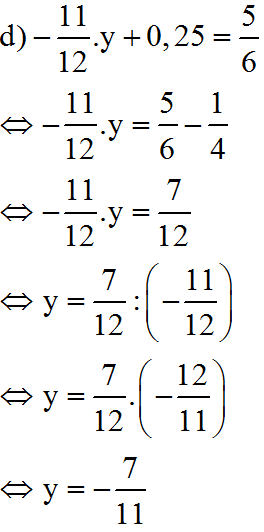Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,-\dfrac{3}{5}.y=\dfrac{21}{10}\)
\(y=\dfrac{21}{10}:\dfrac{-3}{5}=\dfrac{-7}{2}\)
\(b,y:\dfrac{3}{8}=-1\dfrac{31}{33}\)
\(y=-1\dfrac{31}{33}.\dfrac{3}{8}=\dfrac{-8}{11}\)
Vậy \(y=-\dfrac{8}{11}\)
\(c,1\dfrac{2}{5}.y+\dfrac{3}{7}=-\dfrac{4}{5}\)
\(\Rightarrow1\dfrac{2}{5}y=-\dfrac{4}{5}-\dfrac{3}{7}=\dfrac{-43}{35}\)
\(\Rightarrow y=\dfrac{-43}{35}:1\dfrac{2}{5}=\dfrac{-43}{49}\)
\(d,-\dfrac{11}{12}.y+0,25=\dfrac{5}{6}\)
\(\Rightarrow-\dfrac{11}{12}.y=\dfrac{5}{6}-0,25=\dfrac{7}{12}\)
\(\Rightarrow y=\dfrac{7}{12}:\dfrac{-11}{12}=\dfrac{-7}{11}\)

\(a,A=\dfrac{\dfrac{3}{4}-\dfrac{3}{11}+\dfrac{3}{13}}{\dfrac{5}{7}-\dfrac{5}{11}+\dfrac{5}{13}}+\dfrac{\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{4}}{\dfrac{5}{4}-\dfrac{5}{6}+\dfrac{5}{8}}\\ A=\dfrac{\dfrac{405}{572}}{\dfrac{645}{1001}}+\dfrac{\dfrac{5}{12}}{\dfrac{25}{24}}\\ A=\dfrac{189}{172}+\dfrac{2}{5}\\ A=\dfrac{1289}{860}\)

\(xy-3x-y=6\)
\(=>xy+3x-y-3=6-3\)
\(=>x\left(y+3\right)-\left(y+3\right)=3\)
\(=>\left(y+3\right)\left(x-1\right)=3\)
| y+3 | -1 | 3 | 1 | -3 | |
| x-1 | -3 | 1 | 3 | -1 |
| y+3 | -1 | 3 | -3 | 1 |
| y | -4 | -1 | -7 | -3 |
| x-1 | -3 | 1 | 3 | -1 |
| x | -2 | 2 | 4 | 0 |

a) \(\dfrac{x}{5}=\dfrac{y}{6};\dfrac{y}{8}=\dfrac{z}{7}\)và \(x+y-z=69\)
Theo đề bài, ta có:
\(\dfrac{x}{5}=\dfrac{y}{6}\Rightarrow\dfrac{x}{5}\times\dfrac{1}{8}=\dfrac{y}{6}\times\dfrac{1}{8}\Rightarrow\dfrac{x}{40}=\dfrac{y}{48}\)(1)
\(\dfrac{y}{8}=\dfrac{z}{7}\Rightarrow\dfrac{y}{8}\times\dfrac{1}{6}=\dfrac{z}{7}\times\dfrac{1}{6}\Rightarrow\dfrac{y}{48}=\dfrac{z}{42}\)(2)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\Rightarrow\dfrac{x}{40}=\dfrac{y}{48}=\dfrac{z}{42}=\dfrac{x+y-z}{40+48-42}=\dfrac{69}{46}=\dfrac{3}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{40}=\dfrac{3}{2}\Rightarrow x=\dfrac{40\times3}{2}=60\\\dfrac{y}{48}=\dfrac{3}{2}\Rightarrow y=\dfrac{48\times3}{2}=72\\\dfrac{z}{42}=\dfrac{3}{2}\Rightarrow z=\dfrac{42\times3}{2}=63\end{matrix}\right.\)
Vậy \(\Rightarrow\left\{{}\begin{matrix}x=60\\y=72\\z=63\end{matrix}\right.\)
Ta có:\(\dfrac{x}{5}=\dfrac{y}{6}\Rightarrow\dfrac{x}{20}=\dfrac{y}{24}\)(Nhân 2 vế với \(\dfrac{1}{4}\))
\(\dfrac{y}{8}=\dfrac{x}{7}\Rightarrow\dfrac{y}{24}=\dfrac{z}{21}\)(Nhân 2 vế với \(\dfrac{1}{3}\))
\(\Rightarrow\dfrac{x}{20}=\dfrac{y}{24}=\dfrac{z}{21}\)và x+y-z=6
Áp dụng tính chất dãy tỉ số bằng nhau. Ta có:
\(\dfrac{x}{20}=\dfrac{y}{24}=\dfrac{z}{21}=\dfrac{x+y-z}{20+24-21}=\dfrac{69}{23}=3\)
Vì \(\dfrac{x}{20}=3\Rightarrow x=20.3=60\)
\(\dfrac{y}{24}=3\Rightarrow y=24.3=72\)
\(\dfrac{z}{21}=3\Rightarrow z=3.21=63\)
Vậy x=60; y=72; z=63

a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{10}=\dfrac{y}{6}=\dfrac{z}{21}=\dfrac{x+y+z}{10+6+21}=\dfrac{25}{37}\)
Do đó: x=250/37; y=150/37; z=525/37
b: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{\dfrac{3}{2}}=\dfrac{y}{\dfrac{4}{3}}=\dfrac{z}{\dfrac{5}{4}}=\dfrac{x+y+z}{\dfrac{3}{2}+\dfrac{4}{3}+\dfrac{5}{4}}=\dfrac{49}{\dfrac{49}{12}}=12\)
Do đó: x=18; y=16; z=15
c: Ta có: x/2=y/3
nên x/8=y/12(1)
Ta có: y/4=z/5
nên y/12=z/15(2)
Từ (1) và (2) suy ra x/8=y/12=z/15
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}=\dfrac{x+y-z}{8+12-15}=\dfrac{10}{5}=2\)
Do đó: x=16; y=24; z=30

Giải:
a) Theo đề ra, ta có:
\(\dfrac{a}{b}=\dfrac{5}{7}\) và \(a+b=72\) (Sửa x+y =72)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{a}{b}=\dfrac{5}{7}\Leftrightarrow\dfrac{a}{5}=\dfrac{b}{7}\)
\(\Leftrightarrow\dfrac{a}{5}=\dfrac{b}{7}=\dfrac{a+b}{5+7}=\dfrac{72}{12}=6\)
\(\Rightarrow\dfrac{a}{5}=6\Rightarrow a=6.5=30\)
\(\Rightarrow\dfrac{b}{7}=6\Rightarrow b=6.7=42\)
Vậy ...
b) Theo đề ra, ta có:
\(\dfrac{a}{6}=\dfrac{b}{4}=\dfrac{c}{3}\) và \(a+b-c=21\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\Leftrightarrow\dfrac{a}{6}=\dfrac{b}{4}=\dfrac{c}{3}=\dfrac{a+b-c}{6+4-3}=\dfrac{21}{7}=3\)
\(\Rightarrow\dfrac{a}{6}=3\Rightarrow a=3.6=18\)
\(\Rightarrow\dfrac{b}{4}=3\Rightarrow b=3.4=12\)
\(\Rightarrow\dfrac{c}{3}=3\Rightarrow a=3.3=9\)
Vậy ...
c) Theo đề ra, ta có:\(\dfrac{12}{x}=\dfrac{3}{y}\) và \(x-y=36\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{12}{x}=\dfrac{3}{y}\Leftrightarrow\dfrac{x}{12}=\dfrac{y}{3}\)
\(\Leftrightarrow\dfrac{x}{12}=\dfrac{y}{3}=\dfrac{x-y}{12-3}=\dfrac{36}{9}=4\)
\(\Rightarrow\dfrac{x}{12}=4\Rightarrow x=12.4=48\)
\(\Rightarrow\dfrac{y}{3}=4\Rightarrow x=3.4=12\)
Vậy ...
d) Theo đề ra, ta có:
\(\dfrac{a}{2}=\dfrac{b}{5}=\dfrac{c}{7}\) và \(a+b-c=20\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\Leftrightarrow\dfrac{a}{2}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{a+b-c}{2+5-7}=\dfrac{20}{0}=\varnothing\)
Đề câu này sai nhé!
Chúc bạn học tốt!
a) Áp dụng tính chất dãy tỉ số bằng nhau ,ta có :
\(\dfrac{a}{b}=\dfrac{5}{7}\Leftrightarrow\dfrac{a}{5}=\dfrac{b}{7}=\dfrac{a+b}{5+7}=\dfrac{72}{12}=6\)
\(\Rightarrow\left\{{}\begin{matrix}a=5.6=30\\b=7.6=42\end{matrix}\right.\)
b) Áp dụng tính chất dãy tỉ số bằng nhau ,ta có :
\(\dfrac{a}{6}=\dfrac{b}{4}=\dfrac{c}{3}=\dfrac{a+b-c}{6+4-3}=\dfrac{21}{7}=3\)
\(\Rightarrow\left\{{}\begin{matrix}a=6.3=18\\b=4.3=12\\c=3.3=9\end{matrix}\right.\)
c) Áp dụng tính chất dãy tỉ số bằng nhau ,ta có :
\(\dfrac{12}{x}=\dfrac{3}{y}\Leftrightarrow\dfrac{x}{12}=\dfrac{y}{3}=\dfrac{x-y}{12-3}=\dfrac{36}{9}=4\)
\(\Rightarrow\left\{{}\begin{matrix}x=12.4=48\\y=3.4=12\end{matrix}\right.\)
d) Áp dụng tính chất dãy tỉ số bằng nhau ,ta có :
\(\dfrac{a}{2}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{a+b-c}{2+5-7}=\dfrac{20}{0}\) (Vô lý)
=> Không thể làm

\(\dfrac{6}{2x+1}=\dfrac{2}{7}\)
=> 2(2x+1) = 6.7
4x+2=42
4x=40
x=10
Vậy x=10
a)\(\dfrac{6}{2x+1}=\dfrac{2}{7}\\ =>6.7=2.\left(2x+1\right)\\ =>2x+1=\dfrac{6.7}{2}=\dfrac{42}{2}=21\\ =>2x=21-1=20\\ =>x=\dfrac{20}{2}=10\)
b) \(\dfrac{24}{7x-3}=-\dfrac{4}{25}\\ =>24.25=-4.\left(7x-3\right)\\ =>7x-3=\dfrac{24.25}{-4}=-150\\ =>7x=-150+3=-147\\ =>x=\dfrac{-147}{7}=-21\)
c) \(\dfrac{4}{x-6}=\dfrac{y}{24}=-\dfrac{12}{18}\\ =>x-6=\dfrac{4.18}{-12}=-6\\ =>x=-6+6=0\\ y=\dfrac{-12.24}{18}=-16\)
d) \(-\dfrac{1}{5}\le\dfrac{x}{8}\le\dfrac{1}{4}\\ < =>-\dfrac{8}{40}\le-\dfrac{5x}{40}\le\dfrac{10}{40}\\ =>-8\le-5x\le10\\ Mà:-8< -5.1< -5.0< -5.\left(-1\right)< -5.\left(-2\right)=10\\ =>x\in\left\{-2;-1;0;1\right\}\)
e) \(\dfrac{x+46}{20}=x\dfrac{2}{5}\\ < =>\dfrac{x+46}{20}=\dfrac{5x+2}{5}\\ =>5\left(x+46\right)=20\left(5x+2\right)\\ < =>5x+230=100x+40\\ < =>230-40=100x-5x\\ < =>190=95x\\ =>x=\dfrac{190}{95}=2\)
f) \(y\dfrac{5}{y}=\dfrac{56}{y}\\ < =>\dfrac{y^2+5}{y}=\dfrac{56}{y}\\ =>y\left(y^2+5\right)=56y\\ =>y^2+5=\dfrac{56y}{y}=56\\ =>y^2=56-5=51\\ =>y=\sqrt{51}\)