
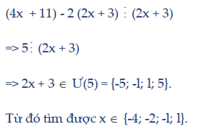
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

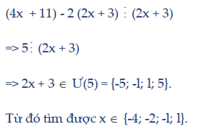

\(a,2x+1⋮x-2\)
\(=>2.\left(x-2\right)+5⋮x-2\)
Do \(2.\left(x-2\right)⋮x-2\)
\(=>5⋮x-2\)
\(=>x-2\inƯ\left(5\right)\)
Nên ta có bảng sau :
| x-2 | 1 | 5 | -1 | -5 |
| x | 3 | 7 | 1 | -3 |
Vậy ...
\(b,3x+5⋮x\)
Do \(3x⋮x=>5⋮x\)
\(=>x\inƯ\left(5\right)\)
Nên ta có bảng sau :
| x | 1 | 5 | -1 | -5 |
Vậy ...
\(c,4x+1⋮2x+3\)
\(=>2.\left(2x+3\right)-5⋮2x+3\)
Do \(2.\left(2x+3\right)⋮2x+3\)
\(=>5⋮2x+3\)
\(=>2x+3\inƯ\left(5\right)\)
Nên ta có bảng sau :
| 2x+3 | 1 | 5 | -1 | -5 |
| 2x | -2 | 2 | -4 | -8 |
| x | -1 | 1 | -2 | -4 |
Vậy ...
a) Ta có: 2x+1=2(x-2)+5
Để 2x+1 chia hết cho x-2 thì 2(x-2)+5 chia hết cho x-2
Vì 2(x-2) chia hết cho x-2
=> 5 chia hết cho x-2
Vì x thuộc Z => z-2 thuộc Ư (5)={-5;-1;1;5}
Nếu x-2=-5 => x=-3
Nếu x-2=-1 => x=1
Nếu x-2=1 => x=3
Nếu x-1=5 => x=6
b) Ta có 3x chia hết cho x với mọi x
=> Để 3x+5 chia hết cho x thì 5 chia hết cho x
Vì x thuộc Z => x thuộc Ư (5)={-5;-1;1;5}
c) Ta có: 4x+11=2(2x+3)+5
Để 4x+11 chia hết cho 2x+3 thì 2(2x+3)+5 chia hết cho 2x+3
Vì 2(2x+3) chia hết cho 2x+3 => 5 chia hết cho 2x+3
Vì x thuộc Z => 2x+3 thuộc Ư (5)={-5;-1;1;5}
Nếu 2x+3=-5 => 2x=-8 => x=-4
Nếu 2x+3=-1 => 2x=-4 => x=-2
Nếu 2x+3=1 => 2x=-2 => x=-1
Nếu 2x+3=5 => 2x=2 => x=1

a) (3x + 5) - 3x chia hết cho x =>5 chia hết cho x hay x Î Ư(5) = {- 5; -1; 1;5}.
b) (4x + 11) - 2 (2x + 3) chia hết cho (2x + 3) => 5 chia hết cho (2x + 3)
=> 2x + 3 Î Ư(5) = {-5; -l; l; 5}. Từ đó tìm được x Î {-4; -2; -l; l}.
c) x (x + 2) - 11chia hết cho (x + 2) => 11 chia hết cho (x + 2)
=> x + 2 ÎƯ (11) = {-11;-1 ;1 ; 11}.
Từ đó tìm được x Î {-13; -3; -l; 9}.


Tham khảo:Tìm x,y thuộc z sao cho 3x+1:hết cho y và 3y+1 :hết cho x?
Bạn phải hiểu một điều đơn giản: với người khác thì vấn đề của họ có ưu tiên số 1. Bạn cần gấp không có nghĩa là họ phải vứt việc của họ để chạy tới giúp. Vì mình có phải cái rốn của vũ trụ đâu. Đấy là chưa kể có người bó tay, có người không muốn giúp.
Mà bạn đóng 1 chủ đề đi. 1 vấn đề thì mở 2 chủ đề để làm gì?
------
Có thể bạn sẽ nói: tôi không cần nữa, nhưng tôi gửi lên vì có thể ai đó cũng quan tâm.
Tôi dùng phương pháp "cần cù"
---------------
1. Ta tìm nghiệm x, y > 0. Ta tìm nghiệm y ≤ x, các nghiệm còn lại có được bằng cách hoán vị x và y
3x + 1 ≥ 3y + 1 = kx, với k là số tự nhiên => k = 1, 2, 4 (3y + 1 không chia hết cho 3)
Với k = 1 => 3y + 1 = x, 3x + 1 = 9y + 4 chia hết cho y <=> 4 chia hết cho y <=> y = 1 và x = 3y + 1 = 4, hoặc y = 2 và x = 3y + 1 = 7, hoặc y = 4 và x = 3y + 1 = 13.
Với k = 2 => 3y + 1 = 2x, 3x + 1 = (9y + 5) / 2 = my (với m tự nhiên)
=> (2m - 9)y = 5 => y là ước của 5 <=> y = 1 và x = (3y + 1) / 2 = 2, hoặc y = 5 và x = (3y + 1) / 2 = 8
Với k = 4 => 3x + 1 ≥ 4x => 1 ≥ x ≥ 1 => x = 1 => 3x + 1 = 4 chia hết cho y <=> y = 1, 2 hoặc 4
=> nghiệm (x, y) = (1, 1), (1, 2), (1, 4), (2, 1), (4, 1), (7, 2), (8, 5), (13, 4) và (hoán vị) (2, 7), (5, 8), (4, 13)
2. Ta tìm 2 nghiệm x, y < 0. Đặt x1 = -x > 0, y1 = -y > 0.
3x + 1 = -3x1 + 1 = - (3x1 - 1) chia hết cho y = -y1, tức (3x1 - 1) chia hết cho y1. Tương tự (3y1 - 1) chia hết cho x1. Ta tìm x ≤ y, tức y1 ≤ x1, các nghiệm còn lại có được bằng cách hoán vị x và y.
3x1 - 1 ≥ 3y1 - 1 = kx1, với k là số tự nhiên => k = 1, 2
Với k = 1=> x1 = 3y1 - 1, 3x1 - 1 = 9y1 - 4 chia hết cho y1 <=> 4 chia hết cho y1 <=> y1 = 1 và x1 = 2, hoặc y1 = 2 và x1 = 5, hoặc y1 = 4 và x1 = 11
Với k = 2 => 3y1 - 1 = 2x1, 3x1 - 1 = (9y1 - 5) / 2 = my1 (với m tự nhiên)
=> (9 - 2m)y1 = 5 => y1 là ước của 5 <=> y1 = 1 và x1 = (3y1 - 1) / 2 = 1, hoặc y1 = 5 và x1 = 7
=> nghiệm (x, y) = (-11, -4), (-7, -5), (-5, -2), (-2, -1), (-1, -1) và (-1, -2), (-2, -5), (-4, -11), (-5, -7)
3. Ta tìm nghiệm y < 0 < x, nghiệm x < 0 < y có được bằng cách hoán vị x và y.
Ta đặt y1 = - y > 0.
3x + 1 chia hết cho y = -y1, tức chia hết cho y1. 3y + 1 = -(3y1 - 1) chia hết cho x, tức (3y1 - 1) chia hết cho x.
3a. y1 ≤ x
3x + 1 ≥ 3y1 + 1 > 3y1 - 1 = kx => k = 1, 2 (3y1 - 1 không chia hết cho 3)
Với k = 1 => x = 3y1 - 1 => 3x + 1 = 9y1 - 2 chia hết cho y1 <=> 2 chia hết cho y1 <=> y1 = 1 và x = 3y1 - 1 = 2 hoặc y1 = 2 và x = 5
Với k = 2 => 3y1 - 1 = 2x => 3x + 1 = (9y1 - 1) / 2 = my1(m tự nhiên)
(9 - 2m)y1 = 1 => y1 = 1 => x = (3y1 - 1) / 2 = 1
=> nghiệm (x, y) = (1, -1), (2, -1), (5, -2)
3b. x < y1
ky1 = 3x + 1 < 3y1 + 1 => k = 1, 2 (3x + 1) không chia hết cho 3)
Với k = 1 => y1 = 3x + 1 => 3y1 - 1 = 9x + 2 chia hết cho x <=> 2 chia hết cho x <=> x = 1 và y1 = 3x + 1 = 4, hoặc x = 2 và y1 = 7
Với k = 2 => 2y1 = 3x + 1 => 3y1 - 1 = (9x + 1) / 2 = mx (m tự nhiên)
=> (2m - 9)x = 1 => x = 1 => y1 = (3x + 1) / 2 = 2
=> nghiệm (x, y) = (1, -2), (1, -4), (2, -7)
Vậy nghiệm x, y khác dấu là: (x, y) = (1, -1), (2, -1), (5, -2), (1, -2), (1, -4), (2, -7) và (hoán vị) (-1, 1), (-1, 2), (-2, 5), (-2, 1), (-4, 1), (-7, 2)
-------------
Kết luận: tất cả các nghiệm:
(x, y) = (-11, -4), (-7, -5), (-7, 2), (-5, -7), (-5, -2), (-4, -11), (-4, 1), (-2, -5), (-2, -1), (-2, 1), (-2, 5), (-1, -2), (-1, -1), (-1, 1), (-1, 2), (1, -4), (1, -2), (1, -1), (1, 1), (1, 2), (1, 4), (2, -7), (2, -1), (2, 1), (2, 7), (4, 1), (4, 13), (5, -2), (5, 8), (7, 2), (8, 5), (13, 4)
-----------
Tất nhiên là tôi chưa kiểm tra lại
bạn ấy cho đề tham khảo sai r
+) 4x+11 chia hết cho x+2
=> 4x+8+3 chia hết cho x+2
=> 4(x+2)+3 chia hết cho x+2
=> 4(x+2) chia hết cho x+2 ; 3 chia hết cho x+2
=> x+2 thuộc Ư(3)={-1,-3,1,3}
=>x={-3,-5,-1,1}
+) 3x-5 chia hết cho x-1
=> 3x-3-2 chia hết cho x-1
=> 3(x-1)-2 chia hết cho x-1
=> 3(x-1) chia hết cho x-1 ; 2 chia hết cho x-1
=> x-1 thuộc Ư(2)={-1,-2,1,2}
=> x={0,-1,2,3}

4x+1 chia hết 2x+2
=>2x+2x+1 chia hết cho 2x+2
=>(2x+2)+(2x+2)+1-4 chia hết 2x+2
=>2(2x+2)-3 chia hết 2x+2 (1)
Có: 2(2x+2) chia hết 2x+2 (2)
(1)(2)=>-3 chia hết 2x+2
=>2x+2 thuộc Ư(-3) và x thuộc Z
=>2x+2 thuộc {1,3,-1,-3}
=>2x thuộc {-1,1,-3,-5}
=>x thuộc {\(\frac{-1}{2}\),\(\frac{1}{2}\),
\(4x+1⋮2x+2\)
\(\Rightarrow2\left(2x+2\right)-3⋮2x+2\)
\(\Rightarrow3⋮2x+2\)(vô lý vì một số lẻ không thể chia hết cho số chẵn)
Vậy không có x thỏa mãn đề bài.