Tìm x, biết: b) 1 1 . 3 + 1 3 . 5 +...

Tìm x, biết:b) 1 1 . 3 +...

H

hieu

24 tháng 8 2019 - olm

TÌM X

a,1/1 nhan 3 + 1/3 nhan 5+1/5 nhan 7+...+1/x nhan (x+2)=20/41

#Toán lớp 6

2

ND

Nguyễn Dương Nguyệt Linh

24 tháng 8 2019

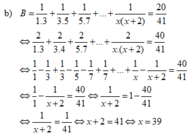
\(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+..+\frac{1}{x\left(x+2\right)}=\frac{20}{41}\)

\(\frac{1}{2}\left(\frac{2}{1.3}+\frac{2}{3.5}+\frac{2}{5.7}+...+\frac{2}{x.\left(x+2\right)}\right)=\frac{20}{41}\)

\(\frac{1}{2}\left(\frac{3-1}{1.3}+\frac{5-3}{3.5}+\frac{7-5}{5.7}+...+\frac{\left(x+2\right)-x}{x\left(x+2\right)}\right)=\frac{20}{41}\)

\(\frac{1}{2}\left(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{x}-\frac{1}{x+2}\right)=\frac{20}{41}\)

\(\frac{1}{2}\left(1-\frac{1}{x+2}\right)=\frac{20}{41}\)

\(1-\frac{1}{x+2}=\frac{20}{41}:\frac{1}{2}\)

\(1-\frac{1}{x+2}=\frac{40}{41}\)

\(\frac{1}{x+2}=1-\frac{40}{41}\)

\(\frac{1}{x+2}=\frac{1}{41}\)

\(x+2=41\)

\(x=41-2\)

\(x=39\)

Đúng(0)

XO

Xyz OLM

24 tháng 8 2019

Tìm x

a) \(\frac{1}{1\times3}+\frac{1}{3\times5}+\frac{1}{5\times7}+...+\frac{1}{x\times\left(x+2\right)}=\frac{20}{41}\)

\(\Rightarrow\frac{1}{2}\times\left(\frac{2}{1\times3}+\frac{2}{3\times5}+\frac{2}{5\times7}+...+\frac{2}{x\times\left(x+1\right)}\right)=\frac{20}{41}\)

\(\Rightarrow\frac{2}{1\times3}+\frac{2}{3\times5}+\frac{2}{5\times7}+...+\frac{2}{x\times\left(x+2\right)}=\frac{20}{41}:\frac{1}{2}\)

\(\Rightarrow\frac{2}{1\times3}+\frac{2}{3\times5}+\frac{2}{5\times7}+...+\frac{2}{x\times\left(x+2\right)}=\frac{40}{41}\)

\(\Rightarrow1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{x}-\frac{1}{\left(x+2\right)}=\frac{40}{41}\)

\(\Rightarrow1-\frac{1}{x+2}=\frac{40}{41}\)

\(\Rightarrow\frac{1}{x+2}=1-\frac{40}{41}\)

\(\Rightarrow\frac{1}{x+2}=\frac{1}{41}\)

\(\Rightarrow x+2=41\)

\(\Rightarrow x=41-2\)

\(\Rightarrow x=39\)

Vậy x = 39

Đúng(0)

N

nguyenhien

11 tháng 8 2015 - olm

Ai giúp em giải bài toán này với:

Tìm x:

1/(1*3)+1/(3*5)+1/(5*7)+....+1/(x*(x+2)) = 20/41

#Toán lớp 6

1

NL

Nguyễn Lương Bảo Tiên

11 tháng 8 2015

\(\frac{1}{1\cdot3}+\frac{1}{3\cdot5}+\frac{1}{5\cdot7}+...+\frac{1}{x\cdot\left(x+2\right)}=\frac{20}{41}\)

\(\frac{1}{2}\cdot\left(\frac{2}{1\cdot3}+\frac{2}{3\cdot5}+\frac{2}{5\cdot7}+...+\frac{2}{x\cdot\left(x+2\right)}\right)=\frac{20}{41}\)

\(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{x}-\frac{1}{x+2}=\frac{20}{41}:\frac{1}{2}\)

\(1-\frac{1}{x+2}=\frac{40}{41}\)

\(\frac{1}{x+2}=1-\frac{40}{41}\)

\(\frac{1}{x+2}=\frac{1}{41}\)

\(\Rightarrow x+2=41\Rightarrow x=39\)

Đúng(0)

DK

Đỗ Khánh Linh

11 tháng 4 2019 - olm

Tìm x;y, biết:

a/( x-7 ).( xy+1 )=9

b/(x+5).(3x-12)>0

c/|x+3|<3

d/-3x+5=41

e/52-|x|=80

g/|7x+1|=20

#Toán lớp 6

6

TT

Trần Thanh Phương

11 tháng 4 2019

Cần bổ sung điều kiện \(x;y\inℤ\)

a) \(\left(x-7\right)\left(xy+1\right)=9=1\cdot9=3\cdot3=\left(-1\right)\cdot\left(-9\right)=\left(-3\right)\cdot\left(-3\right)\)

Xét bảng :

x-7	1	9	-1	-9	3	-3
xy+1	9	1	-9	-1	3	-3
x	8	16	6	-2	10	4
y	1	0	-1,(6)	1	0,2	-1

Vì x,y thuộc Z nên ta có (x;y)={(8;1),(16;0),(-2;1),(4;-1)

Đúng(0)

TT

Trần Thanh Phương

11 tháng 4 2019

b) \(\left(x+5\right)\left(3x-12\right)>0\)

TH1 : \(\hept{\begin{cases}x+5>0\\3x-12>0\end{cases}\Leftrightarrow\hept{\begin{cases}x>-5\\x>4\end{cases}\Leftrightarrow x>4}}\)

TH2 : \(\hept{\begin{cases}x+5< 0\\3x-12< 0\end{cases}\Leftrightarrow\hept{\begin{cases}x< -5\\x< 4\end{cases}\Leftrightarrow x< -5}}\)

Vậy....

Đúng(0)

DT

Đỗ Thị Hoài Ngọc

15 tháng 4 2018 - olm

thực hiện phép tính :

a, -1/2 + 19/23+ -9/2+ 4/23 +3 /-6

b. 5/13+ -5/7 +-20/41 + 8/13 +-21/41

c.-5/7 x 19/41 + 5/7 x -21/41 + 5/7

d. 7/3 +1/2 - -3/70

Đây là phân số

#Toán lớp 6

7

CW

Cure whip

15 tháng 4 2018

A.-9/2

b.-5/7

C.5/287

D.302/105

Đúng(0)

DT

Đỗ Thị Hoài Ngọc

15 tháng 4 2018

nêu cách tính nha bạn

Đúng(0)

TM

trần minh tâm

6 tháng 12 2016 - olm

Bài 1 Tìm x biếtA.89-(73-x)=20B.(x+7)-25=13C.98-(x+4)=20D.140÷(x-8)=7E.4(x+41)=400F.x-[42+(-28)]=-8G.x+5=20-(12--7)H.(x-11)=2.2 mũ 3+20:5I.4(x-3)=7 mũ 2-1 mũ 3J.2 mũ x+1 ×2 mũ 2014=2 mũ 20152x-49=5×3 mũ 2L.3 mũ 2(x+14)-5 mũ 2 =5×2 mũ 2M.6x+x=5 mũ 11 ÷ 5 mũ 9 + 3 mũ 1N.7x-x=5 mũ 21 : 5 mũ 19 +3.2 mũ2 -7 mũ 0O.7x-2x=6 mũ 17 ÷6 mũ 15 + 44 ÷ 11P.3 mũ x =9Q.4 mũ x =64R.9 mũ x-1= 9S.x mũ 4 = 16T.2 mũ x : 2 mũ...

Đọc tiếp

#Toán lớp 6

13

NT

nguyen thanh phong

6 tháng 12 2016

may cai bai day ma cung khong biet oc cho

Đúng(0)

PC

Phong Cách Của Tôi

6 tháng 12 2016

a) 89-(73-x)=20

=>73-x=89-20

=>73-x=69

=>x=73-69

=>x=4

Đúng(0)

A

•ɦà↭ƙĭềυ↭σαηɦ•

10 tháng 3 2019 - olm

1.thực hiện phép tính:

a,5/13 + -5/7 + -20/41 + 8/13 + -21/41

b,-5/7 . 2/11 + -5/7 . 9/11 +1

c, (4/5 + 1/2) . (3/13 - 8/13)

2. a, x + 4/7=7/11

b, -5/6 - x = 7/12 + -1/3

c,x - 1/4 = 5/8 . 2/3

d,x/126 = -5/9 . 4/7

giúp mik vs mn ơi, mik đnag cần rất gấp

#Toán lớp 6

0

M

Maéstrozs

16 tháng 8 2019 - olm

Tìm x biết:

a,(2x+3/5)^2-9/25=0
b,(3x-1).(-1/2x+5)=0
c, (7/5)^x+1-(1/5)^x=-4/625
d,(2/3)^x+2+(2/3)^x+1=20/27

#Toán lớp 6

6

KM

Kiyami Mira

16 tháng 8 2019

a) \(\left(2x+\frac{3}{5}\right)^2-\frac{9}{25}=0\)

\(\left(2x+\frac{3}{5}\right)^2=\frac{9}{25}\)

\(\left(2x+\frac{3}{5}\right)^2=\left(\frac{3}{5}\right)^2\)

\(=>2x+\frac{3}{5}=\frac{3}{5}\)

\(2x=\frac{3}{5}-\frac{3}{5}\)

\(2x=0\)

\(x=0:2\)

\(x=0\)

Đúng(0)

KM

Kiyami Mira

16 tháng 8 2019

b) \(\left(3x-1\right).\left(-\frac{1}{2x}+5\right)=0\)

=> \(\left(3x-1\right)=0\)hoặc \(\left(-\frac{1}{2x}+5\right)=0\)hoặc \(\left(3x-1\right)\)và\(\left(-\frac{1}{2x}+5\right)\)cùng bằng 0.

\(\orbr{\begin{cases}3x-1=0\\-\frac{1}{2x}+5=0\end{cases}}=>\orbr{\begin{cases}3x=1\\-\frac{1}{2x}=-5\end{cases}}=>\orbr{\begin{cases}x\in\varnothing\\2x=\frac{1}{5}\end{cases}}=>x=\frac{1}{5}:2=>x=\frac{1}{10}\)

Đúng(0)

TH

Trần Hà Giang

19 tháng 1 2018 - olm

1 tìm x thuộc Z, biết:

a. 8.( x-| -7|)- 6.( x- 2)= |-8|.6 - 50

b. 2. (4x- 8)- 7.(3+ x) +| -4| . (3-2)

c. 4.( x-5)-7.(5-x)+10.( 5- x)= -3

d. 16.|x-3|- 9.| x-3|= 49

e. 4.|x- 7|-3= -2.|x-7| = 33

2. tính giá trị các tổng sau:

A= -1+3- 5+ 7-.........- 53+55

B= - 1+ 5- 9+ 13-......-41+ 45

3. tìm x, y biết

a. x+y = 10 và x=y

b. 2x+ 3y=180 và x=y

giúp mình với

#Toán lớp 6

0

BJ

Barbie Jenny CHANNEL

14 tháng 12 2017 - olm

1.

30-[ 20 -(5-1) mũ 2] + 42 : 2 - 25

b) 45.37+53:41+63.45+59.53

c) 129[ 4 mũ 2 . 5 - ( -7) ] ; 3

2. tìm x biết

a) x-12=0

b) 2(x-57)-26 =0

c) 3 |x| + 15=78

GIẢI GIÚP MK VỚI IK

#Toán lớp 6

0

HV

hạ vy châu

30 tháng 8 2018 - olm

Tìm x biết

(7.x + 1) : 2 - 23 = 2

(625:x + 4) .29 -80= 41

[ (4.x + 5) : 7 + 5 ] .2 + 16 = 20

#Toán lớp 6

2

EC

Edogawa Conan

30 tháng 8 2018

(7.x + 1) : 2 - 23 = 2

=> (7.x + 1) : 2 = 2 + 23

=> (7.x + 1) : 2 = 25

=> 7.x + 1 = 25 . 2

=> 7.x + 1 = 50

=> 7.x = 50 - 1

=> 7.x = 49

=> x = 49 : 7 = 7

Đúng(0)

A

๖ACE✪Hoàngミ★Việtツ

31 tháng 8 2018

(7.x + 1) : 2 - 23 = 2

=> (7.x + 1) : 2 = 2 + 23

=> 7.x + 1 = 25 . 2

=> 7.x = 50 - 1

=> 7.x = 49

x = 49 : 7 = 7

Vậy.............

hok tốt

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP