Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có đạo hàm y’ = 3x2- 6( m+ 1) x+ 12m.
Hàm số có hai cực trị khi và chỉ khi y’ = 0 có hai nghiệm phân biệt
Hay (m-1) 2> 0 suy ra m≠1 ( *)
Khi đó hai điểm cực trị là A( 2; 9m) : B( 2m; -4m3+ 12m2-3m+ 4).
Tam giác ABC nhận O làm trọng tâm
⇔ 2 + 2 m - 1 = 0 - 4 m 3 + 12 m 2 + 6 m + 4 - 9 2 = 0 ⇔ m = - 1 2 t h ỏ a ( * ) .
Chọn A.

Chọn D
T a c ó y ' = 3 x 2 - 6 ( m + 1 ) x + 12 m
Hàm số có hai cực trị ⇔ y ' = 0 có hai nghiệm phân biệt
![]()
A ( 2 ; 9 m ) , B ( 2 m - 4 m 3 + 12 m 2 - 3 m + 4 )
ABC nhận O làm trọng tâm
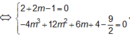
![]()

Lời giải:
Ta có: \(y'=3x^2-6(m+1)x+12m\)
\(y'=0\Leftrightarrow x^2-2(m+1)x+4m=0(*)\)
Nếu $A,B$ là hai điểm cực trị của đths thì $x_A,x_B$ là hai nghiệm của pt $(*)$
Theo định lý Viete: \(x_A+x_B=2(m+1)\)
Nếu $O$ là trọng tâm của tam giác $ABC$ thì:
\(\frac{x_A+x_B+x_C}{3}=x_O=0\Rightarrow \frac{2(m+1)-1}{3}=0\)
\(\Rightarrow m=-\frac{1}{2}\)
Bây giờ ta chỉ cần thử lại với giá trị của $m$ vừa tìm được thì \(\frac{y_A+y_B+y_C}{3}=y_O=0\) hay không (đã ktra và thấy thỏa mãn)
Do đó $m=\frac{-1}{2}$

Bài 1:
\(y=x^4+2(m-4)x^2+m+5\)
\(\Rightarrow y'=4x^3+4(m-4)x\)
\(y'=0\Leftrightarrow x(x^2+m-4)=0\Leftrightarrow \left[\begin{matrix} x=0\\ x^2=4-m\end{matrix}\right.\)
Để đths có 3 điểm cực trị thì \(y'=0\) phải có ít nhất 3 nghiệm pb. Khi đó \(4-m>0\Rightarrow m< 4\)
Khi đó, các điểm cực trị là:
\((0; m+5)\)
\((\sqrt{4-m}, -m^2+9m-11)\)
\((-\sqrt{4-m}, -m^2+9m-11)\)
Nếu $O$ là trọng tâm:
\(\left\{\begin{matrix} \frac{0+\sqrt{4-m}-\sqrt{4-m}}{3}=x_O=0\\ \frac{m+5+2(-m^2+9m-11)}{3}=y_O=0\end{matrix}\right.\)
\(\Leftrightarrow -2m^2+19m-17=0\Rightarrow \left[\begin{matrix} m=\frac{17}{2}\\ m=1\end{matrix}\right.\)
Vì $m< 4$ nên $m=1$
Bài 2:
\(y'=4x^3-4mx=0\Leftrightarrow \left[\begin{matrix}
x=0\\
x^2=m\end{matrix}\right.\)
Để hàm bậc 4 có 3 cực trị thì $y'=0$ phải có 3 nghiệm pb, suy ra $m>0$
Khi đó: \(y'=0\Leftrightarrow \left[\begin{matrix} x=0\\ x=\sqrt{m}\\ x=-\sqrt{m}\end{matrix}\right.\)
Ba điểm cực trị:
\(A(0; m-1)\)
\(B(\sqrt{m}; -m^2+m-1)\)
\(C(-\sqrt{m}; -m^2+m-1)\)
Suy ra:
\(\overrightarrow{BC}=(-2\sqrt{m};0)\); \(\overrightarrow{AB}=(\sqrt{m}; -m^2)\)
\(\overrightarrow{OA}=(0;m-1)\); \(\overrightarrow{OC}=(-\sqrt{m}; -m^2+m-1)\)
Vì $O$ là trực tâm nên : \(\left\{\begin{matrix} \overrightarrow{BC}.\overrightarrow{OA}=0\\ \overrightarrow{AB}.\overrightarrow{OC}=0\end{matrix}\right.\)
\(\Rightarrow \left\{\begin{matrix} -2\sqrt{m}.0+0.(m-1)=0\\ -m+m^2(m^2-m+1)=0\end{matrix}\right.\)
\(\Rightarrow m(m^3-m^2+m-1)=0\)
\(\Leftrightarrow m(m^2+1)(m-1)=0\Rightarrow m=1\) vì \(m>0\)
Vậy.......

a) Xét hàm số \(y=ax^4+bx^2+c\)
Ta có \(y'=4ax^3+2bx=2x\left(2ax^2+b\right)\)
\(y'=0\Leftrightarrow x=0\) hoặc \(2ax^2+b=0\left(1\right)\)
Đồ thị hàm số có 3 cực trị phân biệt khi và chỉ khi \(y'=0\) có 3 nghiệm phân biệt hay phương trình (1) có 2 nghiệm phân biệt khác 0 \(\Leftrightarrow ab< 0\) (*)
Với điều kiện (*) thì đồ thị có 3 điểm cực trị là :
\(A\left(0;c\right);B\left(-\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right);C\left(\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right)\)
Ta có \(AB=AC=\sqrt{\frac{b^2-8ab}{16a^2}};BC=\sqrt{-\frac{2b}{a}}\) nên tam giác ABC vuông khi và chỉ khi vuông tại A.
Khi đó \(BC^2=2AB^2\Leftrightarrow b^3+8a=0\)
Do đó yêu cầu bài toán\(\Leftrightarrow\begin{cases}ab< 0\\b^3+8a=0\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\-8\left(m+1\right)^3+8=0\end{cases}\)\(\Leftrightarrow m=0\)
b) Ta có yêu cầu bài toán \(\Leftrightarrow\begin{cases}ab< 0\\OA=BC\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\m^2-4\left(m+1\right)=0\end{cases}\)
\(\Leftrightarrow m=2\pm2\sqrt{2}\)

nếu có đáp án trắc nghiệm thì theo mình làm bài này nhanh như sau:
tìm tập xác định D=R
tính y', tìm điều kiện để cho hàm số có 3 điểm cực trị là pt y'=0 có 3 nghiệm phân biệt
áp dụng công thức tính nhanh :b^2 -6ac, suy ra m , kết hợp với điều kiện hàm số có 3 điểm cực trị, suy ra m cần tìm
lưu ý: công thức mình đưa ra là b^2-6ac chỉ áp dụng cho hàm bậc 4 trùng phương, 3 điểm cực trị là 3 đỉnh của tam giác và có trọng tâm là gốc tọa độ.

Bài 1: Ta có
\(y'=0\Leftrightarrow x[2mx^2-(m+1)]=0\)
\(\Leftrightarrow \left[\begin{matrix} x=0\\ 2mx^2-(m+1)=0(1)\end{matrix}\right.\)
Một điểm nằm trên trục tọa độ thì tung độ hoặc hoành độ phải bằng $0$. Do đó yêu cầu đề bài được đáp ứng khi $y'=0$ có nghiệm $x=0$ hoặc nếu $x$ khác $0$ thì tung độ tương ứng phải bằng $0$
+) Nếu \(m=0\) : $(1)$ vô nghiệm . $y'=0$ có nghiệm duy nhất $x=0$ (thỏa mãn)
+) Nếu $m=-1$ : $(1)$ có nghiệm $x=0$ (thỏa mãn)
+) Nếu $-1< m< 0$. Từ \((1)\Rightarrow x^2=\frac{m+1}{2m}< 0\) (vô lý) nên $(1)$ vô nghiệm. $y'=0$ có nghiệm duy nhất $x=0$ (thỏa mãn)
+) Nếu \(m>0\) hoặc \(m< -1\)
$(1)$ có 2 nghiệm \(x=\pm \sqrt{\frac{m+1}{2m}}\neq 0\)
\(\Rightarrow y=m(\pm \sqrt{\frac{m+1}{2m}})^4-(m+1)(\pm \sqrt{\frac{m+1}{2m}})^2+(m+1)\)
\(=\frac{(m+1)^2}{4m}-\frac{(m+1)^2}{2m}+(m+1)\)
\(=(m+1)-\frac{(m+1)^2}{4m}=0\)
\(\Leftrightarrow \left[\begin{matrix} m=-1\\ m=\frac{1}{3}\end{matrix}\right.\) . Vì \(\Rightarrow m=\frac{1}{3}\)
Vậy \(-1\leq m\leq 1 \text{or m}=\frac{1}{3}\)
Bài 2:
Ta có: \(y'=4x^3+4mx=0\Leftrightarrow x(x^2+m)=0\)
Nếu $m\geq 0$. PT $y'=0$ có duy nhất nghiệm $x=0$. Ta chỉ thu được 1 điểm cực trị (loại)
Nếu $m<0$. Ngoài $x=0$ pt $y'=0$ còn có 2 nghiệm \(x=\pm \sqrt{-m}\neq 0\)
(thu được 3 cực trị)
Khi đó:
\(y=(\pm \sqrt{-m})^4+2m(\pm \sqrt{-m})^2+4=m^2-2m^2+4=4-m^2\)
Để điểm cực trị nằm trên trục tọa độ thì \(y=0\Leftrightarrow 4-m^2=0\Leftrightarrow m=-2\) (do $m< 0$)
Vậy \(m=-2\)

Chọn D
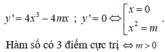
Khi đó đồ thị hàm số có 3 điểm cực trị là:
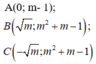
Vì B, C đối xứng với nhau qua trục tung nên B C ⊥ O A
Do đó O là trực tâm tam giác:
![]()
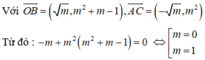
Kết hợp điều kiện, vậy m = 1 là giá trị cần tìm

+ Đạo hàm y’ = 4x3- 4mx
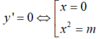
Hàm số có 3 điểm cực trị khi và chỉ khi m≠0.
+ Khi đó đồ thị hàm số có 3 điểm cực trị là:

+ Vì B,C đối xứng nhau qua trục tung nên BC và OA vuông góc với nhau.
Do đó O là trực tâm tam giác ABC khi và chỉ khi OB vuông góc AC hay ![]()
Với
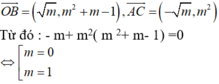
Kết hợp với điều kiện m ≠ 0 thì m = 1 là giá trị cần tìm.
Chọn B.