Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(a) Khi \(m=2,\left(1\right)\Leftrightarrow x^2-4x-5=0\left(2\right)\).
Phương trình (2) có \(a-b+c=1-\left(-4\right)+\left(-5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-1\\x=-\dfrac{c}{a}=5\end{matrix}\right.\).
Vậy: Khi \(m=2,S=\left\{-1;5\right\}\).
(b) Điều kiện: \(x_1,x_2\ne0\Rightarrow m\in R\)
Phương trình có nghiệm khi:
\(\Delta'=\left(-m\right)^2-1\cdot\left(-m^2-1\right)\ge0\)
\(\Leftrightarrow2m^2+1\ge0\left(LĐ\right)\)
Suy ra, phương trình (1) có nghiệm với mọi \(m\).
Theo định lí Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m\\x_1x_2=\dfrac{c}{a}=-m^2-1\end{matrix}\right.\)
Theo đề: \(\dfrac{x_1}{x_2}+\dfrac{x_2}{x_1}=-\dfrac{5}{2}\)
\(\Leftrightarrow\dfrac{x_1^2+x_2^2}{x_1x_2}=-\dfrac{5}{2}\Leftrightarrow\dfrac{\left(x_1+x_2\right)^2-2x_1x_2}{x_1x_2}=-\dfrac{5}{2}\)
\(\Leftrightarrow2\left(x_1+x_2\right)^2+x_1x_2=0\)
\(\Leftrightarrow2\left(2m\right)^2+\left(-m^2-1\right)=0\)
\(\Leftrightarrow7m^2=1\Leftrightarrow m=\pm\dfrac{\sqrt{7}}{7}\) (thỏa mãn).
Vậy: \(m=\pm\dfrac{\sqrt{7}}{7}.\)
bạn giải thích kĩ hộ mik vói cái <=> cuối cùng sao ra như vậy
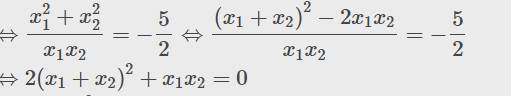

Ta có \(ac=-m^2-2< 0\) ; \(\forall m\) nên pt đã cho luôn có 2 nghiệm trái dấu
Mà \(x_1< x_2\Rightarrow\left\{{}\begin{matrix}x_1< 0\\x_2>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left|x_1\right|=-x_1\\\left|x_2\right|=x_2\end{matrix}\right.\)
\(\Rightarrow2\left|x_1\right|-\left|x_2\right|=4\Leftrightarrow-2x_1-x_2=4\)
Kết hợp với hệ thức Viet: \(x_1+x_2=-m+1\)
\(\Rightarrow\left\{{}\begin{matrix}-2x_1-x_2=4\\x_1+x_2=-m+1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}-x_1=-m+5\\x_1+x_2=-m+1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_1=m-5\\x_2=-2m+6\end{matrix}\right.\)
Thay vào \(x_1x_2=-m^2-2\)
\(\Rightarrow\left(m-5\right)\left(-2m+6\right)=-m^2-2\)
\(\Leftrightarrow m^2-16m+28=0\Rightarrow\left[{}\begin{matrix}m=2\\m=14\end{matrix}\right.\)

a, \(\Delta=m^2-4\left(-4\right)=m^2+16\)> 0
Vậy pt luôn có 2 nghiệm pb
b, Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=-4\end{matrix}\right.\)
Ta có \(\left(x_1+x_2\right)^2-2x_1x_2=5\)
Thay vào ta được \(m^2-2\left(-4\right)=5\Leftrightarrow m^2+3=0\left(voli\right)\)
Bạn ơi, mình có thể hỏi câu c được không ạ? Nếu không được thì không sao, mình cảm ơn câu trả lời của bạn ạ ^-^ chúc bạn một ngày tốt lành nhé.

Lời giải:
Để pt có 2 nghiệm phân biệt thì:
$\Delta'=m^2-(2m-4)=m^2-2m+4>0$
$\Leftrightarrow (m-1)^2+3>0$
$\Leftrightarrow m\in\mathbb{R}$
Áp dụng định lý Viet:
$x_1+x_2=2m$
$x_1x_2=2m-4$
Khi đó:
$x_1+2x_2=8$
$\Leftrightarrow 2m+x_2=8$
$\Leftrightarrow x_2=8-2m$
$\Leftrightarrow x_1=2m-x_2=2m-(8-2m)=4m-8$
$2m-4=x_1x_2=(4m-8)(8-2m)$
$\Leftrightarrow m-2=(2m-4)(8-2m)=2(m-2)(8-2m)$
$\Leftrightarrow (m-2)[2(8-2m)-1]=0$
$\Leftrightarrow (m-2)(15-4m)=0$
$\Leftrightarrow m=2$ hoặc $m=\frac{15}{4}$

\(\Delta=\left[-\left(m+3\right)\right]^2-4\left(2m+2\right)\\ =m^2+6m+9-8m-8\\ =m^2-2m+1\\ =\left(m-1\right)^2\)
de pt co 2 no pb thi Δ >0
<=> (m-1)^2>0
ma \(\left(m-1\right)^2\ge0\forall m\\ \Rightarrow\left(m-1\right)^2\ne0\\ \Leftrightarrow m\ne1\)
Viet: \(x1+x2=m+3\\ x1x2=2m+2\)
0<x1<x2<2\(\Rightarrow\left\{{}\begin{matrix}0< x1+x2< 4\\0< x1x1< 4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}0< m+3< 4\\0< 2m+2< 4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}-3< m< 1\\-1< m< 1\end{matrix}\right.\\ \Leftrightarrow-1< m< 1\)

\(x^2-2\left(m+4\right)x+m^2+8m-9=0\left(1\right)\)
Ta giải \(\Delta=[-2\left(m+4\right)]^2-4\left(m^2+8m-9\right)=100>0\forall m\)
suy ra pt có 2 nghiệm phân biệt \(x_1,x_2\forall m\).
Ta có: \(x_1=m-1\), \(x_2=m+1\) (thay \(\Delta\) vào công thức tìm nghiệm phân biệt).
Gọi \(A=\dfrac{x_1^2+x_2^2-48}{x_1^2+x_2^2}\).
\(\Rightarrow A=1-\dfrac{48}{x_1^2+x_2^2}=1-\dfrac{48}{\left(m-1\right)^2+\left(m+1\right)^2}=1-\dfrac{24}{m^2+1}\).
Để biểu thức A nguyên thì \(\dfrac{24}{m^2+1}\) nguyên, suy ra \(m^2+1\inƯ\left(24\right)\).
\(\Rightarrow m^2+1\in\left\{1;2;4;6;8;12;24\right\}\)
\(\Rightarrow m\in\left\{0;\pm1\right\}\) (vì m nhận giá trị nguyên)
Vậy \(m\in\left\{0;\pm1\right\}\) là giá trị cần tìm.
Mình chỉnh sửa lại một chút nhé.
\(A=1-\dfrac{24}{m^2+2}\)
\(\Rightarrow...\)\(\Rightarrow\)\(m^2+2\in\left\{1;2;3;4;6;8;12;24\right\}\)
\(\Rightarrow m\in\left\{0;\pm1;\pm2\right\}\)
Vậy...

Ta có: \(\text{Δ}=\left(-2m\right)^2-4\cdot1\cdot\left(4m-4\right)\)
\(=4m^2-16m+16=\left(2m-4\right)^2>=0\forall m\)
=>Phương trình luôn có hai nghiệm
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m\\x_1x_2=\dfrac{c}{a}=4m-4\end{matrix}\right.\)
\(x_1^2+x_2^2-8=0\)
=>\(\left(x_1+x_2\right)^2-2x_1x_2-8=0\)
=>\(\left(2m\right)^2-2\left(4m-4\right)-8=0\)
=>\(4m^2-8m=0\)
=>4m(m-2)=0
=>\(\left[{}\begin{matrix}m=0\\m-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=0\\m=2\end{matrix}\right.\)