Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Mức lương bình quân của các cán bộ và nhân viên công ty là số trung bình của bảng lương:
Ý nghĩa: Số trung vị phân chia dãy số liệu sắp thứ tự thành hai phần bằng nhau.

Từ dãy số liệu ta có bảng phân bố tần số - tần suất ghép lớp sau đây:
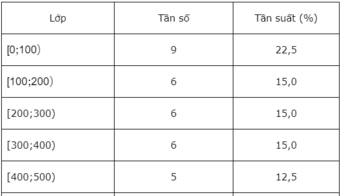
b) b) Cộng các tần suất của bốn lớp [300;400), [400;500), [500;600), [600;700) ta được 15+ 12,5+ 5+ 2,5 = 35. Đáp án là B.

- Mức lương bình quân của các cán bộ và nhân viên công ty là số trung bình của bảng lương:
- Số trung bình:
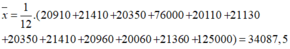
Sắp xếp các số liệu theo dãy tăng dần:
20060; 20110; 20350; 20350; 20910; 20960; 21130; 21360; 21410; 21410; 76000; 125000.
Số trung vị: Me = (20960 + 21130)/2 = 21045.
Ý nghĩa: Số trung vị đại diện cho mức lương trung bình của nhân viên (vì trong trường hợp này chênh lệch giữa các số liệu quá lớn nên không thể lấy mức lương bình quân làm giá trị đại diện).

a) +) Mẫu số liệu đồng bằng sông Hồng:
Số trung bình của mẫu số liệu:
Sắp xếp số liệu trên theo thứ tự không giảm ta được:
23; 27; 34; 35; 37; 39; 46; 54; 57; 57; 187.
Vì n = 11 là số lẻ nên trung bị Q2 = 39.
Nửa số liệu bên trái có tứ phân vị thứ nhất là: Q1 = 34.
Nửa số liệu bên phải có tứ phân vị thứ ba là: Q3 = 57.
Khoảng tứ phân vị là:
ΔQ = Q3 – Q1 = 57 – 34 = 23.
Ta có giá trị lớn nhất của số liệu là 187 và giá trị nhỏ nhất là 23. Khi đó khoảng biến thiên là: R = 187 – 23 = 164.
Theo quan sát số liệu, ta thấy giá trị 57 có tần số suất hiện nhiều nhất nên mốt là 57.
+) Mẫu số liệu đồng bằng sông Cửu Long:
Số trung bình của mẫu số liệu:
Sắp xếp số liệu trên theo thứ tự không giảm ta được:
15; 19; 23; 24; 24; 24; 26; 29; 33; 33; 34; 39; 42.
Vì n = 13 là số lẻ nên trung vị Q2 = 26.
Nửa số liệu bên trái có tứ phân vị thứ nhất là: Q1 = (23 + 24):2 = 23,5.
Nửa số liệu bên phải có tứ phân vị thứ ba là: Q3 = (33 + 34):2 = 33,5.
Khoảng tứ phân vị là:
ΔQ = Q3 – Q1 = 33,5 – 23,5 = 10.
Ta có giá trị lớn nhất của số liệu là 42 và giá trị nhỏ nhất là 15. Khi đó khoảng biến thiên là: R = 42 – 15 = 27.
Theo quan sát số liệu, ta thấy giá trị 24 có tần số suất hiện nhiều nhất nên mốt là 24.
b) Vì trong mẫu số liệu thứ nhất có giá trị bất thường là 187, giá trị này làm ảnh hưởng đến giá trị trung bình của mẫu số liệu một nên có sự sai khác nhiều hai số trung bình của hai mẫu số liệu còn trung vị thì không.
c) Vì trong mẫu số liệu thứ nhất có giá trị bất thường là 187, giá trị này là giá trị lớn nhất nên ảnh hưởng đến khoảng biến thiên của mẫu số liệu một. Trong khi đó, các giá trị của mẫu số liệu hai không có giá trị nào bất thường. Do đó khoảng biến thiên của hai mẫu số liệu có sự chênh lệch nhau.
Độ phân tán của mẫu số liệu một lớn hơn nhiều so với độ phân tán của mẫu số liệu hai. Do đó độ lệch chuẩn của hai số liệu sau có sự khác biệt.
Khoảng tứ phân vị là khoảng biến thiên của 50% số liệu chính giữa mà các giá trị chính giữa của hai mẫu số liệu không quá chênh lệch. Do đó khoảng tứ phân vị của hai mẫu số liệu không quá khác biệt.

Sắp xếp lại mẫu số liệu:
20 120 20 120 21 315 23 405 37 546
Số trung bình:
\(\dfrac{{20120.2 + 21315 + 23405 + 37546}}{5}\)\( = 24501,2\)
Trung vị: 21 315
Mốt: 20 120
Nếu bỏ đi số liệu chỗ ngồi của Sân vận động Quốc gia Mỹ Đình thì số trung bình giảm, trung vị giảm và Mốt thì vẫn giữ nguyên.
Cụ thể: số trung bình là 21 240; trung vị là 20 717,5 và Mốt vẫn là 20 120

Đáp án A
Ta có:
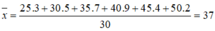
Dựa vào bảng số liệu trên ta thấy giá trị 40 có tần số lớn nhất là 9. Do đó, mốt của mẫu số liệu trên là 40
Giá trị thứ 15,16 của dãy số liệu là 35; 40. Do đó, số trung vị của dãy số liệu là:
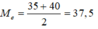

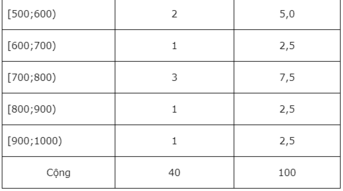
Từ dãy số liệu ta có bảng phân bố tần số - tần suất ghép lớp sau đây:
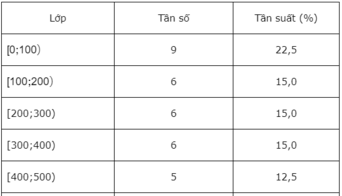
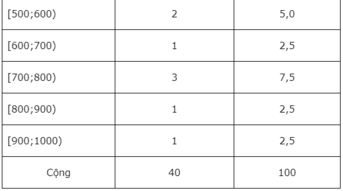
c) Cộng các tần suất của năm lớp [500;600), [600;700), [700;800), [800;900) và [900;1000) ta được . Đáp án là B.

a) Trong bảng phân bố trên, giá trị (tiền lương) 700 (nghìn đồng) và 900 (nghìn đồng) có cùng tần số bằng nhau và lớn hơn các tân số của các giá trị khác. Bảng phân bố này có hai số mốt là:
M1 = 700, M2 = 900.
b) Ý nghĩa: Tỉ lệ công nhân có mức lương 700 nghìn đồng và 900 nghìn đồng cao hơn tỉ lệ công nhân có các mức lương khác.i

Bảng số liệu có 7 giá trị, sắp các giá trị theo thứ tự không giảm ta có:
650, 670, 690, 720, 840, 2500, 3000.
Vì số phần tử = 7 là số lẻ nên số trung vị là Me = 720 (số chính giữa của dãy).
Ý nghĩa: vì số trung bình cộng = 1295,71 cao hơn Me rất nhiều nên trong bài toán này thì sử dụng Me đại diện cho mức lương là hợp lý hơn.



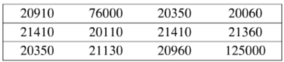
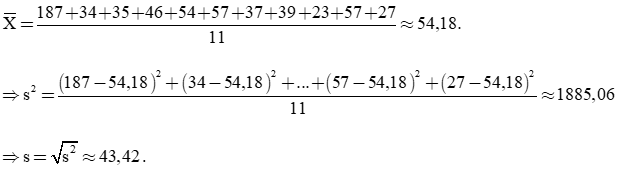
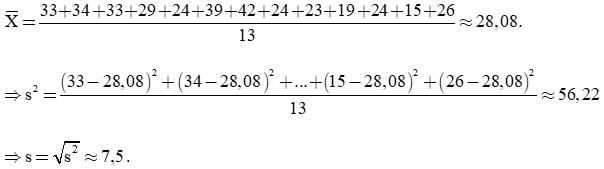


a) Số điểm mà năm vận động viên bóng rổ ghi được trong một trận đấu:
9 8 15 8 20
Số trung bình: \(\overline X = \dfrac{{9 + 8 + 15 + 8 + 20}}{5} = 12\)
Trung vị:
Sắp xếp theo thứ tự không giảm:
8 8 9 15 20
Ta có n=5 là số lẻ nên trung vị là 9.
Mốt: Ta thấy số 8 là số có tần số cao nhất (xuất hiện 2 lần)
Tứ phân vị:
+ Tìm \({Q_2}\)
Ta có trung vị là 9=> \({Q_2} = 9\).
+ Tìm \({Q_1}\)
Nửa số liệu bên trái là:
8 8
Trung vị của mẫu này là \(\dfrac{{8 + 8}}{2} = 8\)=>\({Q_1} = 8\)
+ Tìm \({Q_3}\)
Nửa số liệu bên phải là:
15 20
Trung vị của mẫu này là \(\dfrac{{15 + 20}}{2} = 17,5\)=>\({Q_3} = 17,5\)
Vậy số trung bình là 12, trung vị là 9 và mốt là 8, \({Q_1} = 8\), \({Q_3} = 17,5\)
b) Giá của một số loại giày (đơn vị nghìn đồng):
350 300 650 300 450 500 300 250
Số trung bình: \(\overline X ) \( = \dfrac{{350 + 300.3 + 650 + 450 + 500 + 250}}{8}\) \( = 387,5\)
Trung vị:
Sắp xếp theo thứ tự không giảm:
250 300 300 300 350 450 500 650
Ta có n=8 là số chẵn nên trung vị là trung bình cộng của hai số chính giữa.
Hai số chính giữa là 300 và 350
=> Trung vị là \(\dfrac{{300 + 350}}{2} = 325\)
Mốt: Ta thấy số 300 là số có tần số cao nhất (xuất hiện 3 lần)
Tứ phân vị:
+ Tìm \({Q_2}\)
Ta có trung vị là 325=> \({Q_2} = 325\).
+ Tìm \({Q_1}\)
Vì n chẵn nên nửa số liệu bên trái là:
250 300 300 300
Trung vị của mẫu này là \(\dfrac{{300 + 300}}{2} = 300\)=>\({Q_1} = 300\)
+ Tìm \({Q_3}\)
Vì n chẵn nên nửa số liệu bên phải là:
350 450 500 650
Trung vị của mẫu này là \(\dfrac{{450 + 500}}{2} = 475\)=>\({Q_3} = 475\)
Vậy số trung bình là 387,5, trung vị là 325 và mốt là 300, \({Q_1} = 300\), \({Q_3} = 475\)
c) Số kênh được chiếu của một số hãng truyền hình cáp:
36 38 33 34 32 30 34 35
Số trung bình: \(\overline X = \dfrac{{36 + 38 + 33 + 34.2 + 32 + 30 + 35}}{8} = 34\)
Trung vị:
Sắp xếp theo thứ tự không giảm:
30 32 33 34 34 35 36 38
Ta có n=8 là số chẵn nên trung vị là trung bình cộng của hai số chính giữa.
Hai số chính giữa là 34 và 34
=> Trung vị là 34
Mốt: Ta thấy số 34 là số có tần số cao nhất (xuất hiện 2 lần)
Tứ phân vị:
+ Tìm \({Q_2}\)
Ta có trung vị là 34=> \({Q_2} = 34\).
+ Tìm \({Q_1}\)
Vì n chẵn nên nửa số liệu bên trái là:
30 32 33 34
Trung vị của mẫu này là \(\dfrac{{32 + 33}}{2} = 32,5\)=>\({Q_1} = 32,5\)
+ Tìm \({Q_3}\)
Vì n chẵn nên nửa số liệu bên phải là:
34 35 36 38
Trung vị của mẫu này là \(\dfrac{{35 + 36}}{2} = 35,5\)=>\({Q_3} = 35,5\)
Vậy số trung bình là 34, trung vị là 34 và mốt là 34, \({Q_1} = 32,5\), \({Q_3} = 35,5\)
Chú ý
Nếu n chẵn thì nửa số liệu bên trái (phải) \({Q_2}\) phải chứa cả \({Q_2}\)