Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bước 1: ta tính y'
bước 2: giải pt y'=0 tìm ra xi
bước 3 tính y''
để hàm số có cực đại thì y''(xi)<0
đểhàm số có cực tiểu thì y''(xi)>0
giả các pt ta tìm đc điều kiện của m hàm số có cực đại, cực tiểu

Chọn A.
Ta có y ' = 2 x 3 - 2 m x = 2 x x 2 - m
m > 0 thì y’=0 có ba nghiệm phân biệt và hàm số có một cực tiểu, hai cực đại.
m ≤ 0 thì y’ = 0 có nghiệm duy nhất x = 0 là điểm cực tiểu của hàm số.
Vậy m ≤ 0

Đáp án B
Phương pháp:
Điều kiện để hàm đa thức bậc ba có cực đại, cực tiểu là phương trình y ' = 0 có hai nghiệm phân biệt.
Cách giải:
TH1: m = 0 → y = x − 1 Hàm số không có cực trị.
TH2: TXĐ: D = R
Ta có: y = m x 3 3 − m x 2 + x − 1 ⇒ y ' = m x 2 − 2 m x + 1
Để hàm số cho có cực đại, cực tiểu thì phương trình y ' = 0 phải có 2 nghiệm phân biệt Δ ' = m 2 − m > 0 ⇔ m < 0 m > 1




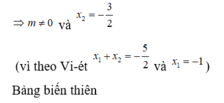
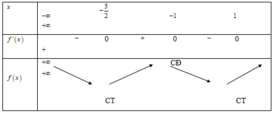
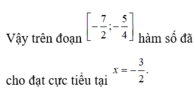





ta có \(y'=4x^3+12mx^2+6\left(m+1\right)x\)
ta giải pt \(4x^3+12mx^2+6\left(m+1\right)x=0\Leftrightarrow x\left(4x^2+12mx+6m+6\right)=0\)
suy ra \(\begin{cases}x=0\\4x^2+12mx+6m+6=0\end{cases}\)
ta tính \(y''=12x^2+24mx+6m+6\)
để hàm số có cực đâị mà ko có cực tiểu thì y''(0)<0 với mọi x
giải pt suy ra đc điều kiện của m