Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(M\left(\frac{1}{2}\right)=a\cdot\left(\frac{1}{2}\right)^2+5\cdot\frac{1}{2}-3=\frac{a}{4}+\frac{10}{4}-3=0\)
\(\frac{a+10}{4}=3\Rightarrow a+10=12\)
\(a=2\)

\(f\left(x\right)=\left(x-1\right)\left(x-3\right)=0\)
\(\Rightarrow\hept{\begin{cases}x-1=0\\x-3=0\end{cases}}\Rightarrow\hept{\begin{cases}x-1\\x-3\end{cases}}\)
=> x = 1 và x = 3 là nghiệm của đa thức f(x)
Mà nghiệm của đa thức f(x) cũng là nghiệm của đa thức g(x)
=> nghiệm của đa thức g(x) là x = { 1; 3 }
Với x = 1 thì \(g\left(x\right)=1^3-a.1^2+b.1-3=0\)
\(\Rightarrow-a+b=2\)(1)
Với x = 3 thì \(g\left(x\right)=3^3-a.3^2+3b-3=0\)
\(\Rightarrow3a-b=8\)(2)
Cộng vế với vế của (1) và (2) ta được : ( - a + b ) + (3a - b) = 10
=> 2a = 10 => a = 5
=> - 5 + b = 2 => b = 7
Vậy a = 5 ; b = 7
(x-1)(x-3)=0
=>x-1=0 hoặc x-3=0
=>x=1 hoặc x=3
Vậy nghiệm của f(x) là 1 và 3
Nghiệm của g(x) cũng là 1 và 3
Với x=1 ta có g(x)=1+a+b-3=0
=>a+b-2=0
a+b=2
Với x=3 ta có g(x)=27-9a+3b-3=0
=>24-9a+3b=0
=>8-3a+b=0
=>3a-b=8
a=\(\frac{8+b}{3}\)
Vậy với a+b=2 hoặc \(a=\frac{8+a}{3}\) thì nghiệm của đa thức f(x) cũng là nghiệm của g(x)

VÌ \(\frac{1}{2}\)là nghiệm của đa thức \(M\left(x\right)\)nên ta có :
\(M\left(\frac{1}{2}\right)=a\cdot\left(\frac{1}{2}\right)^2+5\cdot\frac{1}{2}-3=0\)
\(\Leftrightarrow M\left(\frac{1}{2}\right)=\frac{1}{4}a-\frac{1}{2}=0\)
\(\Rightarrow\frac{1}{4}a=\frac{1}{2}\Rightarrow a=2\)
Vậy hệ số a=2
k cho mình nha bạn !
Vì đa thức M(x) có nghiệm là 1/2 suy ra x=1/2 ta có:
M(1/2)=a.(1/2)2 +5.1/2-3=0
M(1/2)=a.1/4-1/2=0
M(1/2)=a.1/4=1/2
=> a=1/2:1/4=2. Vậy a=2

Nghiệm của đa thức M(x) là \(\dfrac{1}{2}\)
\(\Rightarrow x=\dfrac{1}{2}\) để đa thức M(x) = 0
Thay \(x=\dfrac{1}{2}\), ta có:
\(a.\left(\dfrac{1}{2}\right)^2+5.\dfrac{1}{2}-3=0\\ \Rightarrow\dfrac{1}{4}a+\dfrac{5}{2}=3\\ \Rightarrow\dfrac{1}{4}a=3-\dfrac{5}{2}\\ \Rightarrow\dfrac{1}{4}a=\dfrac{1}{2}\\ \Rightarrow a=\dfrac{1}{2}:\dfrac{1}{4}=2\)
Vậy a = 2. Đa thức M(x) được viết đầy đủ dưới dạng:
\(M\left(x\right)=2x^2+5x-3\)
M(x) có nghiệm là 1/2 nên khi x = 1/2 thì M(x) = 0
\(a\left(\dfrac{1}{2}\right)^2+5.\dfrac{1}{2}-3=0\)
\(\Rightarrow a=2\)
Vậy...

Vì đa thức g(x) là đa thức bậc 3 và mọi nghiệm của f(x) cũng là của g(x) nên:
G/s \(g\left(x\right)=\left(x-1\right)\left(x+3\right)\left(x-c\right)\) \(\left(c\inℝ\right)\)
Khi đó: \(x^3-ax^2+bx-3=\left(x-1\right)\left(x+3\right)\left(x-c\right)\)
\(\Leftrightarrow x^3-ax^2+bx-3=\left(x^2+2x-3\right)\left(x-c\right)\)
\(\Leftrightarrow x^3-ax^2+bx-3=x^3-\left(c-2\right)x^2-\left(2c+3\right)x+3c\)
Đồng nhất hệ số ta được:
\(\hept{\begin{cases}a=c-2\\b=-2c-3\\c=-1\end{cases}}\Leftrightarrow\hept{\begin{cases}a=-3\\b=-1\\c=-1\end{cases}}\)
Vậy a = -3 , b = -1

Theo bài ra ta có: a+2b+4c+1/2=0
(cái này là mẹo nhé: Nhận thấy đơn thức c ko có biến x nên ta sẽ lấy 4 làm thừa số chung.)
=> 4(1/4.a + 1/2.b+c+1/8) = 0
<=> 1/4.a + 1/2.b + c + 1/8 = 0
<=> (1/2)^3 + (1/2)^2. a +1/2.b + c =0
<=> P(1/2) = 0
Vậy 1/2 là 1 nghiệm của đa thức P(x)
Nhớ cái mẹo nhé! ^^

P(x) = ax2 + 5x - 3
Đa thức này có một nghiệm là 1/2 tức là P(1/2) = 0
=> a/4 + 5/2 - 3 = 0
=> a = 2
Đáp số: a = 2
P(x) = ax^2 + 5x - 3
Đa thức này có một nghiệm là 1/2 tức là P(1/2) = 0
=> a/4 + 5/2 - 3 = 0
=> a = 2
Đáp số: a = 2
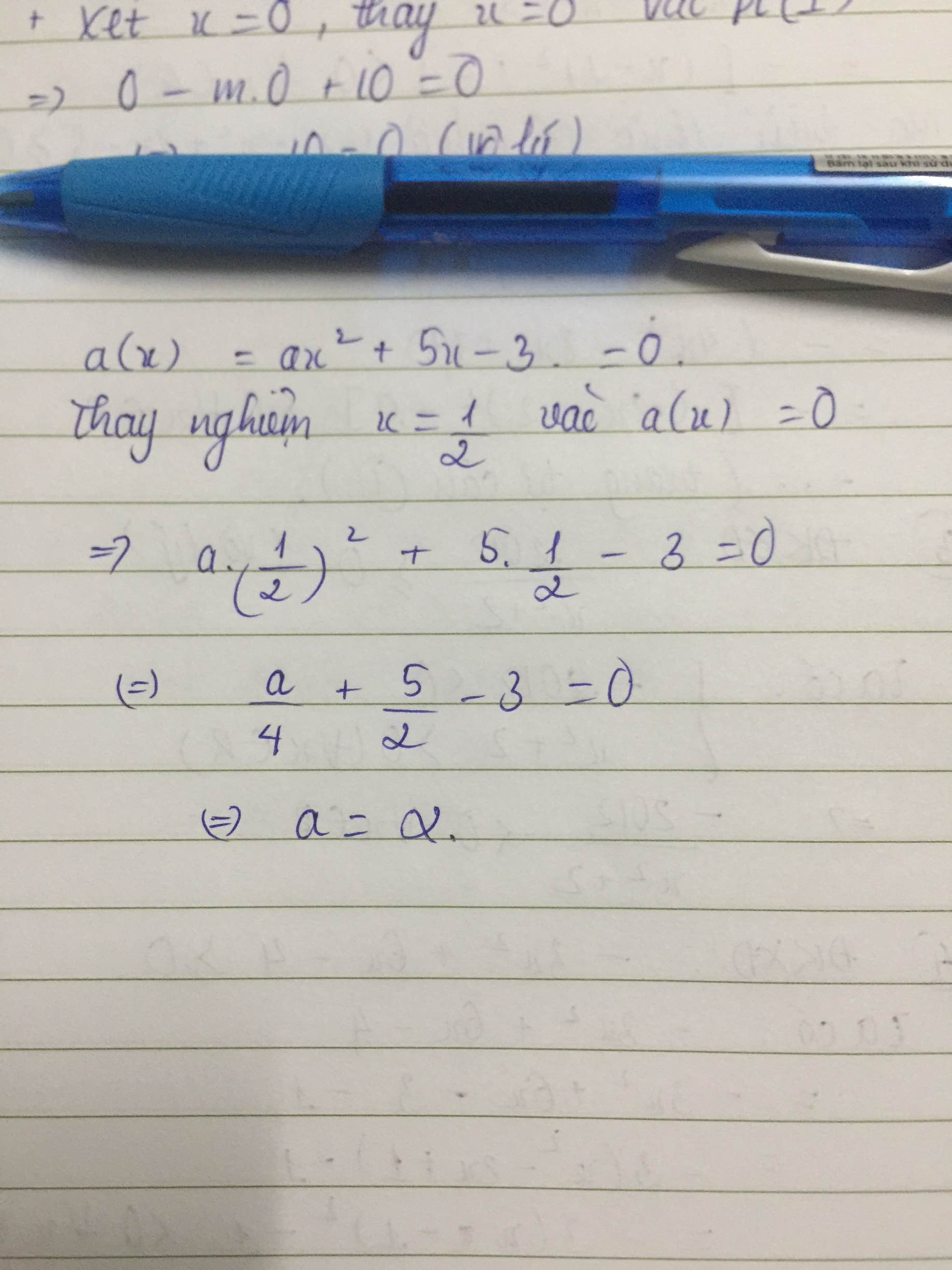
P(x) có nghiệm là 1212 tức là P(1212) = 0 do đó :
a.14+5.12−3=0a.14+5.12−3=0
a.14=3−52a.14=3−52
a14=12a14=12
a=12.4a=12.4
a = 2
Vậy đa thức P(x) =2x2 + 5x - 3
P(x) có nghiệm là \(\dfrac{1}{2}\) tức là P(\(\dfrac{1}{2}\)) = 0 do đó :
a.\(\dfrac{1}{4}\)+5.\(\dfrac{1}{2}\)−3=0
a.\(\dfrac{1}{4}\)=3−\(\dfrac{5}{2}\)
a.\(\dfrac{1}{4}\)=\(\dfrac{1}{2}\)
a=\(\dfrac{1}{2}\).4
a = 2
Vậy đa thức P(x) =2x2 + 5x - 3