Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

3 câu này bạn áp dụng cái này nhé.
`a^2 >=0 forall a`.
`|a| >=0 forall a`.
`1/a` xác định `<=> a ne 0`.
a: P=(x+30)^2+(y-4)^2+1975>=1975 với mọi x,y
Dấu = xảy ra khi x=-30 và y=4
b: Q=(3x+1)^2+|2y-1/3|+căn 5>=căn 5 với mọi x,y
Dấu = xảy ra khi x=-1/3 và y=1/6
c: -x^2-x+1=-(x^2+x-1)
=-(x^2+x+1/4-5/4)
=-(x+1/2)^2+5/4<=5/4
=>R>=3:5/4=12/5
Dấu = xảy ra khi x=-1/2

vì \(\left(2^x+\dfrac{1}{3}\right)^4\) có mũ chẵn là 4 +> \(\left(2^x+\dfrac{1}{3}\right)^4\) > hoặc bằng 0 . Vậy GTNN của \(\left(2^x+\dfrac{1}{3}\right)^4\)= 0 .
vi GTNN cua \(\left(2^x+\dfrac{1}{3}\right)^4\)=> \(\left(2^x+\dfrac{1}{3}\right)^4\)-1 =0 -1=-1
vay GTNN cua \(\left(2^x+\dfrac{1}{3}\right)^4\)-1 =-1
b, vi \(\left(\dfrac{4}{9}x-\dfrac{2}{15}\right)^{2018}\) co mu chan la 2018 => \(\left(\dfrac{4}{9}x-\dfrac{2}{15}\right)^{2018}\) . hoặc bằng 0
Vậy GTLN của \(\left(\dfrac{4}{9}x-\dfrac{2}{15}\right)^{2018}\) = 0 .Vì \(\left(\dfrac{4}{9}x-\dfrac{2}{15}\right)^{2018}\) = 0 =>
\(\left(\dfrac{4}{9}x-\dfrac{2}{15}\right)^{2018}\) +3=0+3=3
Vậy GTLN của \(\left(\dfrac{4}{9}x-\dfrac{2}{15}\right)^{2018}\)+3=3

\(P=\left(0,5-\dfrac{3}{5}\right):\left(-3\right)+\dfrac{1}{3}-\left(-\dfrac{1}{6}\right):\left(-2\right)\)
\(=\left(-\dfrac{1}{2}-\dfrac{3}{5}\right):\left(-3\right)+\dfrac{1}{3}-\left(-\dfrac{1}{6}\right).\left(-\dfrac{1}{2}\right)\)
\(=\left(\dfrac{-5-6}{10}\right):\left(-3\right)+\dfrac{1}{3}-\dfrac{1}{12}\)
\(=-\dfrac{11}{10}:\left(-3\right)+\dfrac{1}{4}\)
\(=-\dfrac{11}{10}.\left(-\dfrac{1}{3}\right)+\dfrac{1}{4}=\dfrac{11}{30}+\dfrac{1}{4}=\dfrac{37}{60}\)
Vậy \(P=\dfrac{37}{60}\)
\(Q=\left(\dfrac{2}{25}-1,008\right):\dfrac{4}{7}:\left[\left(3\dfrac{1}{4}-6\dfrac{5}{9}\right):2\dfrac{2}{17}\right]\)
\(=\left(\dfrac{2}{25}-\dfrac{126}{125}\right):\dfrac{4}{7}:\left[\left(\dfrac{13}{4}-\dfrac{59}{9}\right).\dfrac{36}{17}\right]\)
\(=-\dfrac{116}{125}.\dfrac{7}{4}:\left(-\dfrac{119}{36}.\dfrac{36}{17}\right)\)
\(=\dfrac{-29.7}{125}:\left(-7\right)=\dfrac{29}{125}\)
Vậy \(Q=\dfrac{29}{125}\)

Bạn hãy chỉ giúp mình cách viết phân số và hỗn số trên máy tính. Mình cảm ơn bạn nhiều lắm!![]()
![]()
![]() ^ - ^
^ - ^

\(a,C=\left|\dfrac{1}{3}x+4\right|+1\dfrac{2}{3}\)
Ta có \(\left|\dfrac{1}{3}x+4\right|\ge0\)
\(\Rightarrow\left|\dfrac{1}{3}x+4\right|+1\dfrac{2}{3}\ge1\dfrac{2}{3}\)
Dấu "=" xảy ra khi \(\left|\dfrac{1}{3}x+4\right|=0\)
\(\Leftrightarrow\dfrac{1}{3}x+4=0\)
\(\Leftrightarrow\dfrac{1}{3}x=0-4=-4\)
\(\Leftrightarrow x=-4:\dfrac{1}{3}\)
\(\Leftrightarrow x=-12\)
Vậy \(\min\limits_C=1\dfrac{2}{3}\Leftrightarrow x=-12\)
\(b,D=\left|x-6\right|+\left|x+\dfrac{5}{4}\right|\)
Ta có : \(\left\{{}\begin{matrix}\left|x-6\right|\ge-x+6\\\left|x+\dfrac{5}{4}\right|\ge x+\dfrac{5}{4}\end{matrix}\right.\)
\(\Rightarrow\left|x-6\right|+\left|x+\dfrac{5}{4}\right|\ge-x+6+x+\dfrac{5}{4}=\dfrac{29}{4}\)
Dấu "=" xảy ra khi
\(\left\{{}\begin{matrix}-x+6\ge0\\x+\dfrac{5}{4}\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le6\\x\ge-\dfrac{5}{4}\end{matrix}\right.\)
Vậy \(\min\limits_D=\dfrac{29}{4}\Leftrightarrow-\dfrac{5}{4}\le x\le6\)
b) \(D=\left|x-6\right|+\left|x+\dfrac{5}{4}\right|\)
\(D=\left|6-x\right|+\left|x+\dfrac{5}{4}\right|\ge\left|6-x+x+\dfrac{5}{4}\right|=\dfrac{29}{4}\)
Dấu = xảy ra khi \(\left(6-x\right)\left(x+\dfrac{5}{4}\right)\ge0\Leftrightarrow-\dfrac{5}{4}\le x\le6\)
vậy \(D_{min}=\dfrac{29}{4}\) khi \(-\dfrac{5}{4}\le x\le6\)
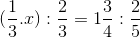
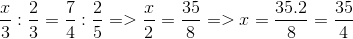
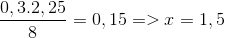

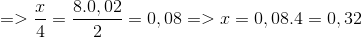
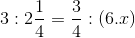
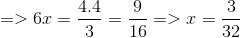
\(D=\left|x+\dfrac{1}{2}\right|+\left|x+\dfrac{1}{3}\right|+\left|x+\dfrac{1}{4}\right|\)
\(=\left|x+\dfrac{1}{2}\right|+\left|x+\dfrac{1}{3}\right|+\left|-\left(x+\dfrac{1}{4}\right)\right|\)
\(=\left|x+\dfrac{1}{2}\right|+\left|x+\dfrac{1}{3}\right|+\left|-x-\dfrac{1}{4}\right|\)
\(\ge x+\dfrac{1}{2}+0-x-\dfrac{1}{4}=\dfrac{1}{4}\)
Đẳng thức xảy ra khi \(x=-\dfrac{1}{3}\)
Vậy với \(x=-\dfrac{1}{3}\) thì \(D_{Min}=\dfrac{1}{4}\)
Ta có : | x + 1/2 | > hoặc = 0
| x + 1/3 | > hoặc = 0
| x + 1/4 | > hoặc = 0
=> D = | x + 1/2 | + | x + 1/3 | + | x + 1/4 | > hoặc = 0
Dấu " = " xảy ra khi D = 0
Vậy GTNN của biểu thức D là 0