NM
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
13 tháng 1 2018
Đáp án A.
Điều kiện x ∈ ℝ
y = cos x + cos x − π 3 = cos x + cos x . cos π 3 + sin x . sin π 3 = cos x + 1 2 cos x + 3 2 sin x
= 3 2 cos x + 3 2 sin x
Cách 1: y = 3 3 2 cos x + 1 2 sin x = 3 sin x + π 3 Suy ra − 3 ≤ y ≤ 3
Vậy m = − 3 ; M = 3 và do đó M 2 + m 2 = 6
Cách 2:
Áp dụng bất đẳng thức Bunyakovsky ta có:
3 2 cos x + 3 2 sin x 2 ≤ 3 2 2 + 3 2 2 cos x 2 + sin x 2
⇔ 3 2 cos x + 3 2 sin x 2 ≤ 3 ⇔ − 3 ≤ y ≤ 3
⇒ M = 3 khi 2 3 cos x = 2 3 sin x 3 2 cos x + 3 2 sin x = 3
Tương tự ta có m = − 3 khi 2 3 cos x = 2 3 sin x 3 2 cos x + 3 2 sin x = − 3
⇒ M 2 + m 2 = 3 2 + − 3 2 = 6
Vậy ta chọn A.
CM
11 tháng 7 2018
Đáp án D
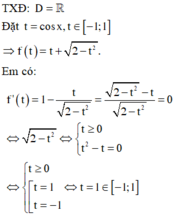
Khi đó em tính được: f(1) = 2; f(-1) = 0. Vậy giá trị lớn nhất của hàm số là 2.
NM
1
30 tháng 9 2015
ta có \(y=2sin^4x+\left(1-2sin^2x\right)^2\)=\(2sin^4x+4sin^4x-4sinx^2+1=6sin^4x-4sin^2x+1\)
đặt \(t=sin^2x,0\le t\le1\)
ta đc \(y=6t^2-4t+1\)
ta tính y'=12t-4
giải pt y'=0 suy ra t=1/3
ta có bảng biến thiên
x y' y 0 1/3 1 0 - + 1 3 1/3
từ bảng bt ta suy ra hàm số đạt giá trị nhỏ nhất \(y=\frac{1}{3}\) khi \(t=\frac{1}{3}\Rightarrow sin^2x=\frac{1}{3}\)
hàm số đạt giá trị lớn nhất y=3 khi \(t=1\Rightarrow sin^2x=1\)
CM
14 tháng 11 2017
Chọn B
Vì sinx-cosx+3>0 nên tập giá trị của hàm số là tập hợp các giá trị của y để phương trình (1-y)sinx+(y+1)cosx=(1+3y) có nghiệm.
Sử dụng điều kiện có nghiệm của phương trình A.sinx+B.cosx=C. Vậy m = -1 và M=1/7
CM
14 tháng 11 2017
Ta có
y = sin x = cos 2 x = sin x - 1 - 2 sin 2 x = 2 sin 2 x + sin x - 1
Đặt t = sin(x), - 1 ≤ t ≤ 1
Ta sẽ đi tìm GTLN và GTNN của hàm số y = g t = 2 t 2 + t - 1 trên đoạn [ -1;1 ]
Ta có g t = - 2 t 3 - t + 1 , - 1 ≤ t ≤ 1 2 2 t 3 + t - 1 , 1 2 ≤ t ≤ 1
* Xét hàm số h t = - 2 t 3 - t + 1 trên đoạn - 1 ; 1 2
Dễ dàng tìm được
M a x r ∈ 1 2 ; 1 h t = 9 8 ⇔ t = - 1 4 M i n r ∈ 1 2 ; 1 h t = 0 ⇔ t = 1 2
* Xét hàm số k t = 2 t 3 + t - 1 trên đoạn 1 2 ; 1
Cũng dễ dàng tìm được
M a x r ∈ 1 2 ; 1 k t = 2 ⇔ t = 1 M i n r ∈ 1 2 ; 1 k t = 0 ⇔ t = 1 2
Qua hai trường hợp trên ta đi đến kết luận
M a x r ∈ - 1 ; 3 g t = 2 ⇔ t = 1 M i n r ∈ - 1 ; 3 g t = 0 ⇔ t = 1 2
Hay
M = M a x y = 2 ⇔ sin x = - 1 ⇔ x = - π 2 + k 2 π m = Miny = 0 ⇔ sin x = 1 2 ⇔ x = π 6 + k 2 π x = 5 π 6 + k 2 π
Đáp án C
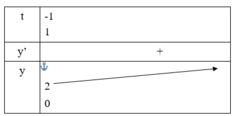
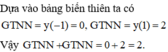
ta có \(y=cosx+2cos^2x-1\)
đặt \(t=cosx\) , \(\left|t\right|\le1\)
ta được \(y=2t^2+t-1\)
\(y'=4t+1\) ta giải phương trình y'=0 suy ra t=-1/4
ta có bbt
x y' y -1 -1/4 1 0 - + 0 2 -9/8
hàm số đạt giá trị lớn nhất =2 khi t =1 hay cosx=1
hàm số đạt giá trị nhỏ nhất =-9/8 khi t=-1/4 hay cosx=-1/4