Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để pt có 2 nghiệm phân biệt và là hai số đối nhau:
\(\Leftrightarrow\hept{\begin{cases}m^4-2m^2+1-m^2-m+2>0\\m\ne-2\\x_1+x_2=0\end{cases}}\)
- \(\orbr{\begin{cases}m< 1\\m>1,546818277\end{cases}}\)
- \(m\ne-2\)
- \(\frac{2m^2-2}{m+2}=0\Rightarrow\orbr{\begin{cases}m=1\left(ktm\right)\\m=-1\left(tm\right)\end{cases}}\)
Vậy ...............

ta có phương trình như sau :
\(x^2+4x+m+3=0\text{ có hai nghiệm âm phân biệt}\Leftrightarrow\)\(\hept{\begin{cases}\Delta'>0\\S< 0\\P>0\end{cases}}\Leftrightarrow\hept{\begin{cases}4-m-3>0\\-4< 0\\m+3>0\end{cases}}\Leftrightarrow1>m>-3\)
vậy có 3 giá trị nguyên của m là 0,-1, -2

Trường hợp 1: m=0
Phương trình sẽ là:
\(0x^2-2\cdot\left(0-1\right)x+0-3=0\)
=>2x-3=0
hay x=3/2
=>Phương trình có đúng một nghiệm dương, còn hai trường hợp còn lại thì ko đúng
Trường hợp 2: m<>0
a:
Để phương trình có hai nghiệm trái dấu thì m(m-3)<0
hay 0<m<3
b:\(\Delta=\left(2m-2\right)^2-4m\left(m-3\right)\)
\(=4m^2-8m+4-4m^2+12m\)
=4m+4
Để phương trình có hai nghiệm dương phân biệt thì \(\left\{{}\begin{matrix}m>-1\\\dfrac{2\left(m-1\right)}{m}>0\\\dfrac{m-3}{m}>0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}-1< m< 0\\m>3\end{matrix}\right.\)
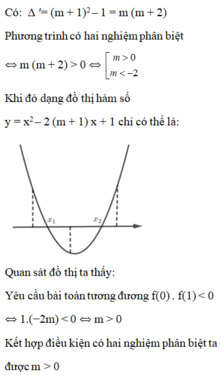
Để phương trình có hai nghiệm phân biệt thì Δ>0
=>m2-4>0
=>m>2 hoặc m<-2