
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

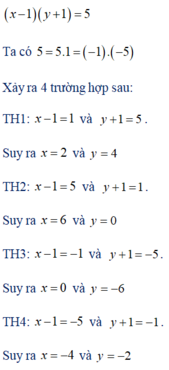


Vì \(\left|x-4\right|\ge0vs\forall x;\left|y+5\right|\ge0vs\forall y\)
\(\Rightarrow\left|x-4\right|+\left|y+5\right|=1\Leftrightarrow\orbr{\begin{cases}\left|x-4\right|=1;\left|y+5=\right|=0\\\left|x-4\right|=0;\left|y+5\right|=1\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x-4=\pm1,y+5=0\\x-4=0;y+5=\pm1\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x-4=3;5;y=-5\\x=4;y=-6;-4\end{cases}}\)
Vậy các cặp (x;y) cần tìm là........................


Vì x,y là số nguyên => |x - 4| là số nguyên
=> |y + 5| là số nguyên
Mà : |x - 4| + |y + 5| = 1
Ta có : 1 = 0 + 1
Th1 :
\(\Leftrightarrow\hept{\begin{cases}\left|x-4\right|=1\\\left|y+5\right|=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x-4=1;-1\\y+5=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=5;3\\y=-5\end{cases}}\)
Th2 :
\(\Leftrightarrow\hept{\begin{cases}\left|x-4\right|=0\\\left|y+5\right|=1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x-4=0\\y+5=1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x-4=0\\y+5=1;-1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=4\\y=-4;-6\end{cases}}\)


\(a,\Leftrightarrow y\left(x+1\right)-3\left(x+1\right)=5\\ \Leftrightarrow\left(x+1\right)\left(y-3\right)=5=5.1=\left(-5\right)\left(-1\right)\\ TH_1:\left\{{}\begin{matrix}x+1=1\\y-3=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=8\end{matrix}\right.\\ TH_2:\left\{{}\begin{matrix}x+1=5\\y-3=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=4\end{matrix}\right.\\ TH_3:\left\{{}\begin{matrix}x+1=-5\\y-3=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-6\\y=2\end{matrix}\right.\\ TH_4:\left\{{}\begin{matrix}x+1=-1\\y-3=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=-2\end{matrix}\right.\)
Vậy \(\left(x;y\right)\in\left\{\left(0;8\right);\left(4;4\right);\left(-6;2\right);\left(-2;-2\right)\right\}\)
\(b,\Leftrightarrow6\left(n-1\right)+11⋮n-1\\ \Leftrightarrow n-1\in\left\{-11;-1;1;11\right\}\\ \Leftrightarrow n\in\left\{-10;0;2;12\right\}\)